My First Python Project
Mathematical Programming Project: Aliquot Sequences
Table of Contents
Introduction
Core Questions:
Core Extensions:
Extensions:
Perfect, Amicable, Adbundant and Deficient Numbers
C. Abundant and Deficient Numbers: Ratio Amongst the Integers
D. Abundant and Deficient Numbers: Existence
E. Abundant and Deficient Numbers: Looping Aliquot Sequences
F. Abundant and Deficient Numbers: General Aliquot Sequences
Conclusion
Introduction
For a positive integer n the sum of proper divisors function is $s(n) = \sum_{\substack{d|n \ d \neq n}} d$.
It gives the sum of all positive divisors of n, excluding n. Interest in this function goes back to the Pythagoreans (6th century B.C.E.). Aliquot sequences are the seqeunces formed by repeatedly applying this function.
Definition: For each n ∈ N the sequence $A_n = {n, s(n), s^2(n), s^3(n),…}$ generated by applying the function s repeatedly is the Aliquot Sequence starting at n. If $s^j(n) = 0$ for some j, the sequence terminates after j.
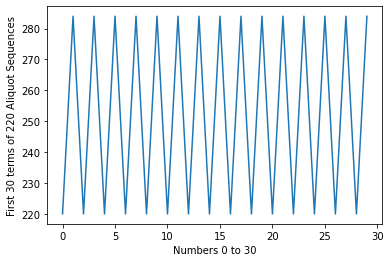
There are some interesting seqeunces. For example, $s(220) = 284$ and $s(284) = 220$. This means ${220, 284, 220, 284, 220, . . .}$ is an infinitely looping aliquot sequence. These are called ‘amicable’ numbers.
Other examples arise from ‘perfect’ numbers such as 6 which has the property that $s(6) = 6$.
There are also sequences which terminate at 0, such as ${7, 1, 0}$. The same should happen starting at any prime.
Surprisingly little is known about aliquot sequences. It is easy to see that there are three possible types of aliquot sequences:
- Those which terminate at zero.
- Those which enter a loop.
- Those which continue infinitely but do not contain repeats.
It is not currently known whether there are any of type 3 but equally it is possible that most aliquot sequences are of this type. The goal of this project is explore these sequences computationally. One of the difficulties is that calculating s(n) becomes computationally difficult once n is large because it involves factoring n into primes.
In this project, we will aim to:
• Write code to compute some aliquot sequences.
• Use this code to explore questions about these sequences.
Remark:
We will define perfect numbers to be a subset of numbers that enter loops, i.e. loops of length 1 still count as loops. This will have implications later on, and would paint a very different picture and ratios if we assumed differently.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# First, run this cell to import the necessary modules
import numpy as np
import matplotlib.pyplot as plt
import timeit
import random
def isprime_basic(n,verbose=False):
'''
Checks whether the argument n is a prime number using a brute force
search for factors between 1 and n. We made it verbose here for
illustration. (I.e. it prints out its results.)
'''
# First, 1 is not prime.
if n == 1:
return False
# If n is even then it is only prime if it is 2
if n % 2 == 0:
if n == 2:
return True
else:
if verbose:
print("{} is not prime: {} is a factor. ".format(n,2))
return False
# So now we can consider odd numbers only.
j = 3
rootN = n**0.5
# Now check all numbers 3,5,... up to sqrt(n)
while j <= rootN:
if n % j == 0:
if verbose:
print("{} is not prime: {} is a factor.".format(n,j))
return False
j = j + 2
if verbose:
print("{} is prime.".format(n))
return True
def smallest_factor(n):
"""Returns the smallest factor of a positive integer n."""
sqrt=n**0.5
i=2
while i<=sqrt:
if n%i==0:
return i #If we get here, return i as the value.
i+=1
return n #If we get through the whole while loop, return n.
def decompose(n):
"""Generates a dictionary representing the prime decomposition."""
factors={}
current_number=n #divide current_number by the factor found found until it reaches 1
while current_number > 1:
p=smallest_factor(current_number)
if p in factors.keys(): #if p is not a new factor, increase the power
factors[p]+=1
else:
factors[p]=1 #if p is a new factor, create a new entry
current_number = current_number//p
return factors
Question 1: The Sum of Proper Divisors
(Core) Write a function to calculate $s(n)$. (Note: In week 9 we’ll see a method that exploits the fact that the sum of all divisors is a multiplicative function.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def slower_s(n):
"""
Given a number n, this function computes s(n), the sum of the proper divisors of n.
"""
# Almost directly adapted from the 'factor_list' function below.
nn=decompose(n)
divisors=[1]
for p in nn.keys():
#This is a list of divisors of p^n.
p_div=[p**i for i in range(1,nn[p]+1)]
newdivisors=[]
#So for each divisor we already have, multiply by each power of p to get new ones.
for pp in p_div:
newdivisors+=[pp*i for i in divisors]
divisors+=newdivisors
s=0
for ss in divisors:
s+=ss
# deal with special value
if n not in (0,1):
return s-n
return "Undefined"
1
2
3
4
5
6
print(slower_s(6))
print(slower_s(220))
print(slower_s(284))
print(slower_s(0))
print('\n')
1
2
3
4
6
284
220
Undefined
Question 2: Generating Aliquot Sequences
(Core) For a given $k$, compute the aliquot sequence starting at $k$ (up to a sensible point).
Practical suggestion: Write your code so that it computes at most the first $n$ terms of the sequence. Also, write it so that for some $i$, your code stops computing new terms once $s^j(k) > i$. At first, you can use lower values but you should aim to get code that runs in a reasonable time for $n$ = 30 and $i$ = $10^9$.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def aliquot_sequence1(n,m=30, i=1e9):
"""
Given a number n, this function computes the first mth terms in its Aliquot Sequence.
Note: 'm' represents length of the Aliquot Sequence returned.
Normally, we use m<=30.
"""
sequence=[n]
for j in range(m-1): # not m since sequence already contains the first term n
nn=slower_s(sequence[j])
if nn == "Undefined":
sequence.append(0) # we first check the case for n=0, with s(0) = Undefined
return sequence
elif nn>i: # if a term of the sequence exceeds input i, we stop generating terms and return the shortened sequence
return sequence
#elif nn == sequence[j]:
#return sequence
# we could include the lines above to ensure sequences stop once they reach a term that will repeat
# however, we comment them out so that graphs in further questions are more clear and easy to read
else:
sequence.append(nn) # otherwise we append s(n) in a loop
return sequence
1
aliquot_sequence1(6, 10)
1
[6, 6, 6, 6, 6, 6, 6, 6, 6, 6]
1
print(aliquot_sequence1(220))
1
[220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284]
1
print(aliquot_sequence1(220, 30, 250))
1
[220]
1
aliquot_sequence1(25, 10)
1
[25, 6, 6, 6, 6, 6, 6, 6, 6, 6]
1
print(aliquot_sequence1(72))
1
[72, 123, 45, 33, 15, 9, 4, 3, 1, 0]
1
2
print(aliquot_sequence1(138, 30, 1e6))
print(len(aliquot_sequence1(138, 30, 1e6)))
1
2
[138, 150, 222, 234, 312, 528, 960, 2088, 3762, 5598, 6570, 10746, 13254, 13830, 19434, 20886, 21606, 25098, 26742, 26754, 40446, 63234, 77406, 110754, 171486, 253458, 295740, 647748]
28
1
2
3
4
5
6
7
8
9
10
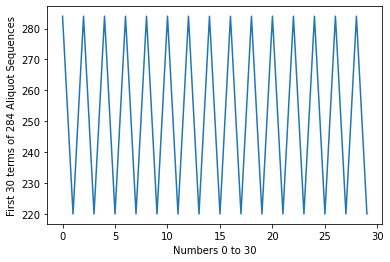
print(len(aliquot_sequence1(220,30)))
print(aliquot_sequence1(220,30))
print(aliquot_sequence1(284,30))
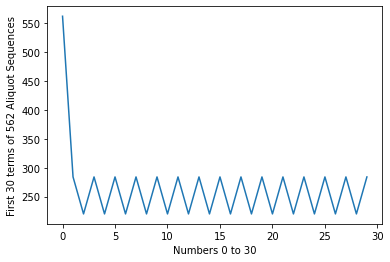
print(aliquot_sequence1(562,30))
print(aliquot_sequence1(400,5))
1
2
3
4
5
30
[220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284]
[284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220]
[562, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284]
[400, 561, 303, 105, 87]
Question 3: Detecting Loops
(Core) Find a way to detect loops. (There’s a little bit to this - look at the sequence starting at 562 to see why.)
We found 2 ways to do this: check whether a term repeats, or compare the size of the set to the length of the sequence. We kept both functions to test their running time, and indeed the second is more efficient.
1
2
3
4
5
6
7
8
9
10
11
12
def detect_loop(n,m=30,i=1e9):
"""
Given n, checks whether its Aliquot Sequence enters a loop (returns True)
or not (returns False) by checking whether terms are repeated within the first m terms.
"""
# The meaning is, firstly use 'n' and 'm' to form an aliquot sequence, and then detect whether there's a loop
u=aliquot_sequence1(n,m)
for i in range(1,len(u)): # we check whether a term is repeated in the Aliquot Sequence
for j in range(i-1):
if u[i]==u[j]:
return True # if so, return True, otherwise return False
return False
1
2
3
4
5
6
7
8
9
10
11
12
13
# A more easy version of detect_loop(n,m)
def seq_detect_loop1(n, m=30, i=1e9):
"""
Given an n, this function detects whether its Aliquot Sequence
reaches a loop within its first m terms (and exceeds i).
It returns True if it does, and False if it doesn't.
"""
ali_seq = aliquot_sequence1(n, m, i)
if len(set(ali_seq)) == len(ali_seq): # more efficient- checks whether the size of the set
return False # and sequence are the same; if not a term must be repeated, so loop
elif ali_seq[-1] == 0: # but if loop entered is at 0, we exclude this, so we check that the last term is not 0
return False
return True
1
2
3
4
print("Time to calculate detect_loop(19977):")
%timeit detect_loop(19977)
print("Time to calculate seq_detect_loop1(19977):")
%timeit seq_detect_loop1(19977)
1
2
3
4
Time to calculate detect_loop(19977):
97.7 µs ± 581 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Time to calculate seq_detect_loop1(19977):
94.3 µs ± 863 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Though the time difference is not too considerable, the new function has to check less values and is more efficient, both in terms of time and space.
1
print(aliquot_sequence1(562))
1
[562, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284]
1
2
3
print(seq_detect_loop1(220))
print(seq_detect_loop1(562))
1
2
True
True
1
2
print(seq_detect_loop1(72))
print(aliquot_sequence1(72))
1
2
False
[72, 123, 45, 33, 15, 9, 4, 3, 1, 0]
Question 4: Classifying Aliquot Sequences
(Core) For each $k$ < 20000 try to classify it according to the end state of the aliquot sequence starting at k. It should either terminate at zero, enter a loop or be unknown (you might want to distinguish between the cases where the calculation was cut short because you reached term $n$ and those where the sequece exceeded $i$).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def classify_ali_seq_4(k,m=30,i=1e9):
"""
For the first k Aliquot Sequences, this function classifies
them into those which, within the first m terms:
1) Enter a loop.
2) Terminate at 0.
3) Exceed input number i and never repeat.
4) Have done none of the above when they reach term m
(i.e. are likely to have been "cut short").
It returns the labelled list for each category.
"""
loop = []
terminated = []
exceeded = []
reached_term = []
for j in range(1,k+1): # first k numbers
u = aliquot_sequence1(j,m,i)
if seq_detect_loop1(j) == True: # use previous function to detect loops
loop.append(j)
elif u[-1] == 0: # check whether terminates at 0 by checking the last term
terminated.append(j)
elif len(u) != m: # if sequence is cut short, either exceeds i
# or terminates at 0, but this comes after 0's if statement
exceeded.append(j)
else:
reached_term.append(j) # otherwise, appended to the undecided category
return f'Numbers that enter a loop: {loop} \n\nNumbers that terminated at 0: {terminated} \n\nNumbers that exceeded i: {exceeded} \n\nNumbers that reached term m, the input: {reached_term}'
1
print(classify_ali_seq_4(200))
1
2
3
4
5
6
7
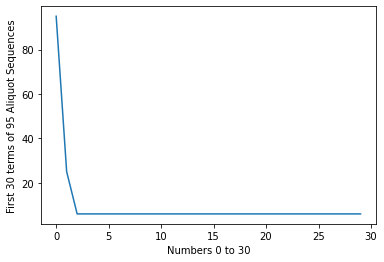
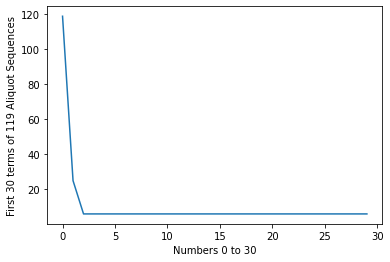
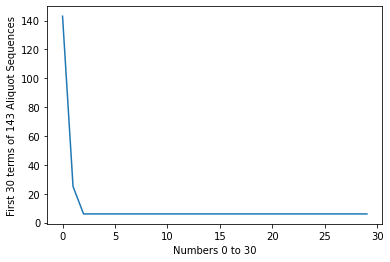
Numbers that enter a loop: [6, 25, 28, 95, 119, 143]
Numbers that terminated at 0: [1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 139, 140, 141, 142, 144, 145, 146, 147, 148, 149, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200]
Numbers that exceeded i: []
Numbers that reached term m, the input: [138, 150, 168, 180]
1
2
print(aliquot_sequence1(28, 30))
print(aliquot_sequence1(119, 30))
1
2
[28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28]
[119, 25, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6]
1
2
print(aliquot_sequence1(138, 30))
print(len(aliquot_sequence1(138)))
1
2
[138, 150, 222, 234, 312, 528, 960, 2088, 3762, 5598, 6570, 10746, 13254, 13830, 19434, 20886, 21606, 25098, 26742, 26754, 40446, 63234, 77406, 110754, 171486, 253458, 295740, 647748, 1077612, 1467588]
30
1
print(aliquot_sequence1(136, 30))
1
[136, 134, 70, 74, 40, 50, 43, 1, 0]
Question 5: Classifying Aliquot Sequences More Efficiently
(Core) If your code takes too long to do (4) for this range for $k$ revisit steps (1) and (2).
We redefine the functions s(n), aliquot_sequence(n,m,i), and seq_detect_loop(n,m,i): We will use the memory to store values so the functions call them and run faster. We keep the old versions of the functions to compare running time and conclude whether our new functions are indeed more efficient, even though this does take up more space.
We now also modify the function to be able to print the classified lists as well as allowing us to pick a certain category and produce only that list, so that we can use this later.
1
2
3
4
5
6
7
8
9
10
11
MEMO={} # we introduce the use of memory, as a dictionary to keep track of the corresponding inputs in the form n:s(n)
def s(n):
"""
Given a number n, this function computes s(n), the sum of the proper divisors of n.
"""
if n in MEMO:
return MEMO[n]
else:
MEMO[n]=slower_s(n)
return slower_s(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def aliquot_sequence(n,m=30, i=1e9):
"""
Given a number n, this function computes the first mth terms in its Aliquot Sequence.
Note: 'm' represents length of the Aliquot Sequence returned.
Normally, we use m<=30.
"""
sequence=[n]
for j in range(m-1):
nn=s(sequence[j]) # uses new, better function s
if nn == "Undefined":
sequence.append(0)
return sequence
elif nn>i:
return sequence
#elif nn == sequence[j]:
#return sequence
# we could include the lines above to ensure sequences stop once they reach a term that will repeat
# however, we comment them out so that graphs in further questions are more clear and easy to read
else:
sequence.append(nn)
return sequence
1
2
3
4
5
6
7
8
9
10
11
12
def seq_detect_loop(n, m=30, i=1e9):
"""
Given an n, this function detects whether its Aliquot Sequence
reaches a loop within its first m terms (and exceeds i).
It returns True if it does, and False if it doesn't.
"""
ali_seq = aliquot_sequence(n, m, i) # uses new, better aliquot_sequence function
if len(set(ali_seq)) == len(ali_seq):
return False
elif ali_seq[-1] == 0:
return False
return True
1
2
3
4
5
6
7
8
9
10
def classify_loops(k, m=30, i=1e9):
"""
For the first k Aliquot Sequences, this function returns a list of the numbers
that enter a loop within the first m terms.
"""
loop_list = []
for j in range(1,k+1):
if seq_detect_loop(j) == True: # uses our previous functions to detect loops
loop_list.append(j) # and appends them to a list
return loop_list
1
2
3
4
5
6
7
8
9
10
11
def classify_terminated(k, m=30, i=1e9):
"""
For the first k Aliquot Sequences, this function returns a list of the numbers
that terminate at 0 within the first m terms.
"""
terminated_list = []
for j in range(1,k+1):
u = aliquot_sequence(j,m,i) # as above, checks the last term is 0 for terminating sequences
if u[-1] == 0:
terminated_list.append(j)
return terminated_list
1
2
3
4
5
6
7
8
9
10
11
def classify_exceeded(k, m=30, i=1e9):
"""
For the first k Aliquot Sequences, this function returns a list of the numbers
that exceed input i within the first m terms.
"""
exceeded_list = []
for j in range(1,k+1):
u = aliquot_sequence(j,m,i)
if len(u) != m and u[-1] != 0: # again, if the length is not m
exceeded_list.append(j) # and doesn't terminate at 0, must have exceeded i
return exceeded_list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def classify_reached_term(k, m=30, i=1e9):
"""
For the first k Aliquot Sequences, this function returns a list of the numbers
that neither enter a loop, nor terminate at 0, nor exceed input i within the first m terms
(i.e. are likely to have been "cut short").
"""
reached_term_list = [j for j in range(1, k+1)] # all the left over numbers after removing the other categories
for elt in classify_loops(k, m, i):
if elt in reached_term_list:
reached_term_list.remove(elt)
for elt in classify_terminated(k, m, i):
if elt in reached_term_list:
reached_term_list.remove(elt)
for elt in classify_exceeded(k, m, i):
if elt in reached_term_list:
reached_term_list.remove(elt)
return reached_term_list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def classify_ali_seq_5(k,m=30,i=1e9):
"""
Similar to classify_aliq_seq_4.
For the first k Aliquot Sequences, this function classifies
them into those which, within the first m terms:
1) Enter a loop.
2) Terminate at 0.
3) Exceed input number i and never repeat.
4) Have done none of the above when they reach term m
(i.e. are likely to have been "cut short").
It returns the labelled list for each category,
but it is more efficient because it does so by calling other functions.
"""
# uses above functions to print lists for each category
loop = classify_loops(k, m, i)
terminated = classify_terminated(k, m, i)
exceeded = classify_exceeded(k, m, i)
reached_term = classify_reached_term(k, m, i)
return f"Numbers that enter a loop: {loop} \n\nNumbers that terminated at 0: {terminated} \n\nNumbers that exceeded i: {exceeded} \n\nNumbers that reached term m, the input: {reached_term}"
1
classify_ali_seq_5(100,m=30,i=1e9)
1
'Numbers that enter a loop: [6, 25, 28, 95] \n\nNumbers that terminated at 0: [1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 96, 97, 98, 99, 100] \n\nNumbers that exceeded m: [] \n\nNumbers that reached term m, the input: []'
1
classify_ali_seq_5(20000,m=30,i=1e9)
Click to expand
'Numbers that enter a loop: [6, 25, 28, 95, 119, 143, 220, 284, 417, 445, 496, 562, 565, 608, 650, 652, 675, 685, 783, 790, 909, 913, 1064, 1177, 1184, 1188, 1210, 1235, 1294, 1308, 1336, 1380, 1420, 1441, 1443, 1490, 1574, 1595, 1604, 1633, 1690, 1692, 1715, 1717, 1772, 1778, 1816, 1898, 2008, 2122, 2152, 2162, 2172, 2173, 2195, 2225, 2362, 2387, 2541, 2542, 2581, 2582, 2620, 2630, 2652, 2676, 2678, 2725, 2863, 2924, 2930, 2950, 2974, 3124, 3142, 3162, 3202, 3277, 3278, 3286, 3311, 3332, 3337, 3350, 3528, 3575, 3596, 3693, 3712, 3750, 3850, 3888, 3899, 3938, 3944, 3999, 4118, 4141, 4156, 4180, 4317, 4372, 4404, 4448, 4522, 4535, 4717, 4739, 4763, 4775, 4790, 4840, 4897, 4930, 5020, 5024, 5078, 5150, 5158, 5234, 5243, 5380, 5564, 5603, 5605, 5622, 5630, 5634, 5854, 5855, 5890, 5900, 5942, 5960, 6028, 6036, 6099, 6123, 6145, 6232, 6242, 6280, 6368, 6420, 6532, 6612, 6658, 6663, 6672, 6694, 6808, 6872, 6876, 7006, 7025, 7106, 7120, 7130, 7149, 7180, 7186, 7227, 7294, 7380, 7396, 7403, 7418, 7514, 7520, 7524, 7527, 7540, 7543, 7587, 7694, 7796, 7856, 7860, 7885, 7923, 7930, 7940, 8076, 8104, 8128, 8135, 8306, 8320, 8354, 8470, 8477, 8480, 8545, 8593, 8776, 8784, 8785, 8924, 9035, 9038, 9068, 9204, 9299, 9322, 9332, 9370, 9464, 9484, 9550, 9572, 9574, 9620, 9653, 9683, 9699, 9921, 9997, 10031, 10042, 10070, 10100, 10127, 10178, 10188, 10235, 10294, 10312, 10462, 10596, 10624, 10648, 10678, 10682, 10688, 10713, 10742, 10744, 10796, 10828, 10856, 11092, 11186, 11225, 11242, 11260, 11312, 11376, 11398, 11518, 11630, 11702, 11724, 11748, 11768, 11794, 11878, 11905, 11921, 11932, 11963, 11966, 11986, 11999, 12032, 12034, 12084, 12142, 12285, 12288, 12308, 12314, 12428, 12443, 12458, 12484, 12496, 12554, 12636, 12682, 12692, 12724, 12752, 12860, 13055, 13058, 13100, 13186, 13189, 13221, 13279, 13282, 13334, 13382, 13453, 13496, 13525, 13587, 13595, 13738, 13756, 13786, 13833, 13923, 13960, 13984, 14023, 14032, 14042, 14065, 14146, 14156, 14188, 14194, 14206, 14228, 14254, 14264, 14277, 14285, 14288, 14316, 14338, 14350, 14354, 14416, 14428, 14488, 14528, 14536, 14595, 14650, 14696, 14752, 14786, 14816, 15034, 15056, 15074, 15119, 15188, 15203, 15224, 15340, 15364, 15382, 15472, 15476, 15544, 15552, 15586, 15622, 15656, 15660, 15670, 15706, 15716, 15719, 15777, 15792, 15830, 15854, 15874, 15880, 15950, 15979, 15998, 16039, 16096, 16198, 16202, 16256, 16306, 16312, 16355, 16383, 16384, 16544, 16634, 16636, 16644, 16655, 16750, 16813, 16814, 16849, 16898, 16934, 17143, 17152, 17187, 17206, 17210, 17243, 17277, 17296, 17316, 17384, 17413, 17496, 17530, 17540, 17553, 17596, 17667, 17716, 17831, 17944, 18038, 18070, 18156, 18332, 18350, 18416, 18492, 18551, 18577, 18604, 18625, 18638, 18659, 18688, 18696, 18736, 18746, 18770, 18854, 18916, 18922, 18932, 19024, 19094, 19116, 19126, 19133, 19190, 19198, 19294, 19312, 19336, 19474, 19491, 19564, 19573, 19690, 19744, 19916, 19922, 19933, 19940, 19958, 19977] \n\nNumbers that terminated at 0: [1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 139, 140, 141, 142, 144, 145, 146, 147, 148, 149, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 211, 212, 213, 214, 215, 216, 217, 218, 219, 221, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 277, 278, 279, 280, 281, 282, 283, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 307, 308, 309, 310, 311, 313, 314, 315, 316, 317, 319, 320, 321, 322, 323, 324, 325, 326, 327, 328, 329, 331, 332, 333, 334, 335, 336, 337, 338, 339, 340, 341, 342, 343, 344, 345, 346, 347, 348, 349, 350, 351, 352, 353, 355, 356, 357, 358, 359, 361, 362, 363, 364, 365, 367, 368, 369, 370, 371, 372, 373, 374, 375, 376, 377, 379, 380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391, 392, 393, 394, 395, 397, 398, 399, 400, 401, 402, 403, 404, 405, 406, 407, 408, 409, 410, 411, 412, 413, 414, 415, 416, 418, 419, 420, 421, 422, 423, 424, 425, 426, 427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439, 440, 441, 442, 443, 444, 446, 447, 448, 449, 450, 451, 452, 453, 454, 455, 457, 458, 459, 460, 461, 462, 463, 464, 465, 466, 467, 468, 469, 470, 471, 472, 473, 474, 475, 476, 477, 478, 479, 481, 482, 483, 484, 485, 486, 487, 488, 489, 490, 491, 492, 493, 494, 495, 497, 499, 500, 501, 502, 503, 504, 505, 506, 507, 508, 509, 511, 512, 513, 514, 515, 516, 517, 518, 519, 520, 521, 522, 523, 524, 525, 526, 527, 529, 530, 531, 532, 533, 535, 536, 537, 538, 539, 540, 541, 542, 543, 544, 545, 547, 548, 549, 550, 551, 553, 554, 555, 556, 557, 558, 559, 560, 561, 563, 566, 567, 568, 569, 571, 572, 573, 574, 575, 576, 577, 578, 579, 580, 581, 583, 584, 585, 586, 587, 588, 589, 590, 591, 592, 593, 595, 596, 597, 598, 599, 601, 602, 603, 604, 605, 606, 607, 609, 610, 611, 613, 614, 615, 616, 617, 618, 619, 620, 621, 622, 623, 624, 625, 626, 627, 628, 629, 630, 631, 632, 633, 634, 635, 636, 637, 638, 639, 640, 641, 643, 644, 645, 646, 647, 648, 649, 651, 653, 655, 656, 657, 658, 659, 661, 662, 663, 664, 665, 666, 667, 668, 669, 670, 671, 672, 673, 674, 676, 677, 678, 679, 680, 681, 682, 683, 684, 686, 687, 688, 689, 690, 691, 692, 693, 694, 695, 697, 698, 699, 700, 701, 703, 704, 705, 706, 707, 708, 709, 710, 711, 712, 713, 714, 715, 716, 717, 718, 719, 721, 722, 723, 724, 725, 727, 728, 729, 730, 731, 732, 733, 734, 735, 736, 737, 738, 739, 740, 741, 742, 743, 744, 745, 746, 747, 748, 749, 751, 752, 753, 754, 755, 756, 757, 758, 759, 760, 761, 762, 763, 764, 765, 766, 767, 768, 769, 770, 771, 772, 773, 774, 775, 776, 777, 778, 779, 781, 782, 784, 785, 787, 788, 789, 791, 792, 793, 794, 795, 796, 797, 799, 800, 801, 802, 803, 804, 805, 806, 807, 808, 809, 810, 811, 812, 813, 814, 815, 816, 817, 818, 819, 820, 821, 823, 824, 825, 826, 827, 829, 830, 831, 832, 833, 835, 836, 837, 838, 839, 841, 842, 843, 844, 845, 847, 848, 849, 850, 851, 852, 853, 854, 855, 856, 857, 859, 860, 861, 862, 863, 865, 866, 867, 868, 869, 871, 872, 873, 874, 875, 876, 877, 878, 879, 880, 881, 882, 883, 884, 885, 886, 887, 889, 890, 891, 892, 893, 894, 895, 896, 897, 898, 899, 900, 901, 902, 903, 904, 905, 906, 907, 908, 910, 911, 912, 914, 915, 916, 917, 918, 919, 920, 921, 922, 923, 924, 925, 926, 927, 928, 929, 931, 932, 933, 934, 935, 937, 938, 939, 940, 941, 942, 943, 944, 945, 946, 947, 948, 949, 950, 951, 952, 953, 954, 955, 956, 957, 958, 959, 961, 962, 963, 964, 965, 967, 968, 969, 970, 971, 972, 973, 974, 975, 976, 977, 979, 980, 981, 982, 983, 984, 985, 986, 987, 988, 989, 991, 992, 993, 994, 995, 997, 998, 999, 1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010, 1011, 1012, 1013, 1014, 1015, 1016, 1017, 1018, 1019, 1020, 1021, 1022, 1023, 1024, 1025, 1027, 1028, 1029, 1030, 1031, 1033, 1034, 1035, 1036, 1037, 1038, 1039, 1040, 1041, 1042, 1043, 1045, 1046, 1047, 1048, 1049, 1050, 1051, 1052, 1053, 1054, 1055, 1056, 1057, 1058, 1059, 1060, 1061, 1063, 1065, 1066, 1067, 1068, 1069, 1070, 1071, 1072, 1073, 1075, 1076, 1077, 1078, 1079, 1080, 1081, 1082, 1083, 1084, 1085, 1087, 1088, 1089, 1090, 1091, 1092, 1093, 1094, 1095, 1096, 1097, 1099, 1100, 1101, 1102, 1103, 1105, 1106, 1107, 1108, 1109, 1110, 1111, 1112, 1113, 1114, 1115, 1116, 1117, 1118, 1119, 1120, 1121, 1123, 1124, 1125, 1126, 1127, 1128, 1129, 1130, 1131, 1132, 1133, 1135, 1136, 1137, 1138, 1139, 1140, 1141, 1142, 1143, 1144, 1145, 1147, 1149, 1150, 1151, 1152, 1153, 1154, 1155, 1156, 1157, 1159, 1160, 1161, 1162, 1163, 1164, 1165, 1166, 1167, 1168, 1169, 1171, 1172, 1173, 1174, 1175, 1176, 1178, 1179, 1180, 1181, 1182, 1183, 1185, 1186, 1187, 1189, 1190, 1191, 1192, 1193, 1194, 1195, 1196, 1197, 1198, 1199, 1200, 1201, 1202, 1203, 1205, 1206, 1207, 1208, 1209, 1211, 1212, 1213, 1214, 1215, 1216, 1217, 1219, 1220, 1221, 1222, 1223, 1224, 1225, 1226, 1227, 1228, 1229, 1231, 1232, 1233, 1234, 1236, 1237, 1238, 1239, 1240, 1241, 1242, 1243, 1244, 1245, 1246, 1247, 1249, 1250, 1251, 1252, 1253, 1254, 1255, 1256, 1257, 1258, 1259, 1261, 1262, 1263, 1264, 1265, 1267, 1268, 1269, 1270, 1271, 1272, 1273, 1274, 1275, 1276, 1277, 1279, 1280, 1281, 1282, 1283, 1284, 1285, 1286, 1287, 1288, 1289, 1291, 1292, 1293, 1295, 1296, 1297, 1298, 1299, 1300, 1301, 1303, 1304, 1305, 1306, 1307, 1309, 1310, 1311, 1312, 1313, 1315, 1317, 1318, 1319, 1321, 1322, 1323, 1324, 1325, 1327, 1328, 1329, 1330, 1331, 1332, 1333, 1334, 1335, 1337, 1339, 1340, 1341, 1342, 1343, 1344, 1345, 1346, 1347, 1348, 1349, 1351, 1352, 1353, 1354, 1355, 1357, 1358, 1359, 1360, 1361, 1363, 1364, 1365, 1366, 1367, 1368, 1369, 1370, 1371, 1373, 1375, 1376, 1377, 1378, 1379, 1381, 1382, 1383, 1384, 1385, 1387, 1388, 1389, 1390, 1391, 1393, 1394, 1395, 1396, 1397, 1399, 1400, 1401, 1402, 1403, 1404, 1405, 1406, 1407, 1408, 1409, 1411, 1412, 1413, 1414, 1415, 1416, 1417, 1418, 1419, 1421, 1423, 1424, 1425, 1426, 1427, 1429, 1430, 1431, 1432, 1433, 1434, 1435, 1436, 1437, 1438, 1439, 1442, 1444, 1445, 1446, 1447, 1448, 1449, 1450, 1451, 1452, 1453, 1454, 1455, 1456, 1457, 1458, 1459, 1460, 1461, 1462, 1463, 1465, 1466, 1467, 1468, 1469, 1470, 1471, 1472, 1473, 1474, 1475, 1477, 1478, 1479, 1480, 1481, 1483, 1484, 1485, 1486, 1487, 1489, 1491, 1492, 1493, 1495, 1496, 1497, 1498, 1499, 1500, 1501, 1502, 1503, 1504, 1505, 1507, 1508, 1509, 1510, 1511, 1513, 1514, 1515, 1516, 1517, 1519, 1520, 1522, 1523, 1524, 1525, 1526, 1527, 1528, 1529, 1531, 1532, 1533, 1534, 1535, 1536, 1537, 1538, 1539, 1540, 1541, 1543, 1544, 1545, 1546, 1547, 1548, 1549, 1550, 1551, 1552, 1553, 1555, 1556, 1557, 1558, 1559, 1561, 1562, 1563, 1564, 1565, 1566, 1567, 1568, 1569, 1570, 1571, 1573, 1575, 1576, 1577, 1579, 1580, 1581, 1582, 1583, 1584, 1585, 1586, 1587, 1588, 1589, 1591, 1592, 1593, 1594, 1597, 1598, 1599, 1600, 1601, 1602, 1603, 1605, 1606, 1607, 1609, 1610, 1611, 1612, 1613, 1614, 1615, 1616, 1617, 1618, 1619, 1621, 1622, 1623, 1624, 1625, 1626, 1627, 1628, 1629, 1630, 1631, 1634, 1635, 1636, 1637, 1638, 1639, 1640, 1641, 1642, 1643, 1644, 1645, 1646, 1647, 1648, 1649, 1651, 1652, 1653, 1654, 1655, 1657, 1658, 1659, 1660, 1661, 1663, 1664, 1665, 1666, 1667, 1668, 1669, 1670, 1671, 1672, 1673, 1675, 1676, 1677, 1678, 1679, 1681, 1682, 1683, 1684, 1685, 1687, 1688, 1689, 1691, 1693, 1694, 1695, 1696, 1697, 1699, 1700, 1701, 1702, 1703, 1705, 1706, 1707, 1708, 1709, 1711, 1712, 1713, 1714, 1716, 1718, 1719, 1720, 1721, 1723, 1724, 1725, 1726, 1727, 1728, 1729, 1730, 1731, 1732, 1733, 1735, 1736, 1737, 1738, 1739, 1740, 1741, 1742, 1743, 1744, 1745, 1746, 1747, 1748, 1749, 1750, 1751, 1752, 1753, 1754, 1755, 1756, 1757, 1759, 1760, 1761, 1762, 1763, 1764, 1765, 1766, 1767, 1768, 1769, 1771, 1773, 1774, 1775, 1776, 1777, 1779, 1780, 1781, 1783, 1784, 1785, 1786, 1787, 1788, 1789, 1790, 1791, 1792, 1793, 1795, 1796, 1797, 1798, 1799, 1800, 1801, 1802, 1803, 1804, 1805, 1807, 1808, 1809, 1810, 1811, 1812, 1813, 1814, 1815, 1817, 1819, 1821, 1822, 1823, 1824, 1825, 1826, 1827, 1828, 1829, 1830, 1831, 1832, 1833, 1834, 1835, 1837, 1838, 1839, 1840, 1841, 1843, 1844, 1845, 1846, 1847, 1849, 1850, 1851, 1852, 1853, 1855, 1856, 1857, 1858, 1859, 1861, 1862, 1863, 1864, 1865, 1867, 1868, 1869, 1870, 1871, 1873, 1874, 1875, 1877, 1879, 1880, 1881, 1882, 1883, 1884, 1885, 1886, 1887, 1888, 1889, 1891, 1892, 1893, 1894, 1895, 1897, 1899, 1900, 1901, 1903, 1904, 1905, 1906, 1907, 1908, 1909, 1910, 1911, 1912, 1913, 1915, 1916, 1917, 1918, 1919, 1921, 1922, 1923, 1924, 1925, 1926, 1927, 1928, 1929, 1930, 1931, 1933, 1934, 1935, 1936, 1937, 1939, 1940, 1941, 1942, 1943, 1945, 1946, 1947, 1948, 1949, 1951, 1952, 1953, 1954, 1955, 1956, 1957, 1958, 1959, 1960, 1961, 1963, 1964, 1965, 1966, 1967, 1968, 1969, 1970, 1971, 1972, 1973, 1974, 1975, 1976, 1977, 1978, 1979, 1980, 1981, 1982, 1983, 1984, 1985, 1987, 1988, 1989, 1990, 1991, 1993, 1994, 1995, 1996, 1997, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2009, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023, 2024, 2025, 2026, 2027, 2028, 2029, 2030, 2031, 2032, 2033, 2034, 2035, 2036, 2037, 2038, 2039, 2041, 2042, 2043, 2044, 2045, 2047, 2048, 2049, 2050, 2051, 2052, 2053, 2054, 2055, 2056, 2057, 2059, 2060, 2061, 2062, 2063, 2064, 2065, 2066, 2067, 2068, 2069, 2070, 2071, 2072, 2073, 2074, 2075, 2076, 2077, 2078, 2079, 2080, 2081, 2083, 2084, 2085, 2086, 2087, 2089, 2090, 2091, 2092, 2093, 2095, 2096, 2097, 2098, 2099, 2100, 2101, 2102, 2103, 2104, 2105, 2107, 2108, 2109, 2110, 2111, 2113, 2114, 2115, 2116, 2117, 2118, 2119, 2120, 2121, 2123, 2125, 2126, 2127, 2128, 2129, 2130, 2131, 2132, 2133, 2134, 2135, 2137, 2138, 2139, 2140, 2141, 2143, 2144, 2145, 2146, 2147, 2148, 2149, 2150, 2151, 2153, 2155, 2156, 2157, 2158, 2159, 2161, 2163, 2164, 2165, 2167, 2168, 2169, 2170, 2171, 2174, 2175, 2176, 2177, 2178, 2179, 2180, 2181, 2182, 2183, 2184, 2185, 2186, 2187, 2188, 2189, 2191, 2192, 2193, 2194, 2196, 2197, 2198, 2199, 2200, 2201, 2203, 2204, 2205, 2206, 2207, 2209, 2210, 2211, 2213, 2215, 2216, 2217, 2218, 2219, 2220, 2221, 2222, 2223, 2224, 2227, 2228, 2229, 2230, 2231, 2233, 2234, 2235, 2236, 2237, 2239, 2240, 2241, 2242, 2243, 2244, 2245, 2246, 2247, 2248, 2249, 2251, 2252, 2253, 2254, 2255, 2257, 2258, 2259, 2260, 2261, 2263, 2264, 2265, 2266, 2267, 2269, 2270, 2271, 2272, 2273, 2274, 2275, 2276, 2277, 2278, 2279, 2281, 2282, 2283, 2284, 2285, 2286, 2287, 2288, 2289, 2290, 2291, 2293, 2294, 2295, 2296, 2297, 2299, 2300, 2301, 2302, 2303, 2304, 2305, 2306, 2307, 2308, 2309, 2311, 2312, 2313, 2314, 2315, 2316, 2317, 2318, 2319, 2320, 2321, 2323, 2324, 2325, 2326, 2327, 2329, 2330, 2331, 2332, 2333, 2335, 2336, 2337, 2338, 2339, 2341, 2342, 2343, 2344, 2345, 2347, 2348, 2349, 2350, 2351, 2353, 2354, 2355, 2357, 2359, 2361, 2363, 2364, 2365, 2366, 2367, 2368, 2369, 2371, 2372, 2373, 2374, 2375, 2376, 2377, 2378, 2379, 2380, 2381, 2383, 2384, 2385, 2386, 2388, 2389, 2390, 2391, 2392, 2393, 2395, 2396, 2397, 2398, 2399, 2400, 2401, 2403, 2404, 2405, 2407, 2408, 2409, 2410, 2411, 2412, 2413, 2414, 2415, 2416, 2417, 2419, 2420, 2421, 2422, 2423, 2425, 2426, 2427, 2428, 2429, 2431, 2432, 2433, 2434, 2435, 2437, 2438, 2439, 2440, 2441, 2443, 2444, 2445, 2446, 2447, 2449, 2450, 2451, 2452, 2453, 2454, 2455, 2456, 2457, 2458, 2459, 2460, 2461, 2462, 2463, 2464, 2465, 2466, 2467, 2468, 2469, 2470, 2471, 2473, 2474, 2475, 2476, 2477, 2479, 2481, 2482, 2483, 2485, 2486, 2487, 2488, 2489, 2491, 2492, 2493, 2494, 2495, 2496, 2497, 2498, 2499, 2500, 2501, 2503, 2504, 2505, 2506, 2507, 2508, 2509, 2510, 2511, 2512, 2513, 2515, 2516, 2517, 2518, 2519, 2520, 2521, 2522, 2523, 2524, 2525, 2527, 2528, 2529, 2530, 2531, 2532, 2533, 2534, 2535, 2536, 2537, 2539, 2540, 2543, 2545, 2546, 2547, 2548, 2549, 2551, 2552, 2553, 2554, 2555, 2556, 2557, 2558, 2559, 2560, 2561, 2563, 2564, 2565, 2566, 2567, 2569, 2570, 2571, 2572, 2573, 2575, 2576, 2577, 2578, 2579, 2583, 2584, 2585, 2586, 2587, 2588, 2589, 2590, 2591, 2592, 2593, 2594, 2595, 2596, 2597, 2598, 2599, 2600, 2601, 2602, 2603, 2605, 2606, 2607, 2608, 2609, 2610, 2611, 2612, 2613, 2614, 2615, 2617, 2618, 2619, 2621, 2623, 2624, 2625, 2626, 2627, 2628, 2629, 2631, 2632, 2633, 2634, 2635, 2636, 2637, 2638, 2639, 2641, 2642, 2643, 2644, 2645, 2646, 2647, 2648, 2649, 2650, 2651, 2653, 2654, 2655, 2656, 2657, 2659, 2661, 2662, 2663, 2665, 2666, 2667, 2668, 2669, 2671, 2672, 2673, 2674, 2675, 2677, 2679, 2680, 2681, 2683, 2684, 2685, 2686, 2687, 2688, 2689, 2690, 2691, 2692, 2693, 2694, 2695, 2696, 2697, 2698, 2699, 2700, 2701, 2702, 2703, 2704, 2705, 2706, 2707, 2708, 2709, 2710, 2711, 2713, 2714, 2715, 2717, 2719, 2720, 2721, 2722, 2723, 2726, 2727, 2728, 2729, 2730, 2731, 2732, 2733, 2734, 2735, 2736, 2737, 2738, 2739, 2740, 2741, 2743, 2744, 2745, 2746, 2747, 2748, 2749, 2750, 2751, 2752, 2753, 2755, 2756, 2757, 2758, 2759, 2761, 2762, 2763, 2764, 2765, 2767, 2768, 2769, 2770, 2771, 2773, 2774, 2775, 2776, 2777, 2779, 2780, 2781, 2782, 2783, 2785, 2786, 2787, 2788, 2789, 2791, 2792, 2793, 2794, 2795, 2796, 2797, 2798, 2799, 2800, 2801, 2803, 2804, 2805, 2806, 2807, 2809, 2810, 2811, 2812, 2813, 2815, 2816, 2817, 2818, 2819, 2821, 2822, 2823, 2824, 2825, 2827, 2829, 2830, 2831, 2832, 2833, 2834, 2835, 2836, 2837, 2839, 2841, 2842, 2843, 2844, 2845, 2846, 2847, 2848, 2849, 2851, 2852, 2853, 2854, 2855, 2857, 2858, 2859, 2860, 2861, 2865, 2866, 2867, 2868, 2869, 2870, 2871, 2872, 2873, 2875, 2876, 2877, 2878, 2879, 2881, 2882, 2883, 2885, 2887, 2888, 2889, 2890, 2891, 2892, 2893, 2894, 2895, 2896, 2897, 2899, 2900, 2901, 2902, 2903, 2905, 2906, 2907, 2908, 2909, 2911, 2913, 2914, 2915, 2916, 2917, 2918, 2919, 2920, 2921, 2923, 2925, 2926, 2927, 2928, 2929, 2931, 2932, 2933, 2935, 2936, 2937, 2938, 2939, 2941, 2942, 2943, 2944, 2945, 2947, 2948, 2949, 2951, 2953, 2954, 2955, 2956, 2957, 2959, 2961, 2962, 2963, 2964, 2965, 2966, 2967, 2968, 2969, 2971, 2972, 2973, 2975, 2977, 2978, 2979, 2980, 2981, 2983, 2984, 2985, 2986, 2987, 2988, 2989, 2990, 2991, 2992, 2993, 2994, 2995, 2997, 2998, 2999, 3001, 3002, 3003, 3004, 3005, 3006, 3007, 3008, 3009, 3010, 3011, 3013, 3014, 3015, 3016, 3017, 3019, 3020, 3021, 3022, 3023, 3026, 3027, 3028, 3029, 3031, 3032, 3033, 3034, 3035, 3037, 3038, 3039, 3041, 3042, 3043, 3044, 3045, 3046, 3047, 3049, 3051, 3053, 3054, 3055, 3056, 3057, 3058, 3059, 3061, 3062, 3063, 3064, 3065, 3066, 3067, 3068, 3069, 3070, 3071, 3072, 3073, 3074, 3075, 3076, 3077, 3079, 3081, 3082, 3083, 3085, 3086, 3087, 3088, 3089, 3090, 3091, 3092, 3093, 3094, 3095, 3096, 3097, 3098, 3099, 3100, 3101, 3103, 3104, 3105, 3106, 3107, 3109, 3110, 3111, 3112, 3113, 3115, 3116, 3117, 3118, 3119, 3121, 3122, 3123, 3125, 3127, 3128, 3129, 3130, 3131, 3133, 3134, 3135, 3136, 3137, 3139, 3140, 3141, 3143, 3145, 3146, 3147, 3148, 3149, 3151, 3152, 3153, 3154, 3155, 3157, 3158, 3159, 3160, 3161, 3163, 3164, 3165, 3166, 3167, 3169, 3170, 3171, 3173, 3175, 3176, 3177, 3178, 3179, 3180, 3181, 3182, 3183, 3184, 3185, 3187, 3188, 3189, 3190, 3191, 3193, 3194, 3195, 3196, 3197, 3199, 3200, 3201, 3203, 3205, 3206, 3207, 3208, 3209, 3211, 3212, 3213, 3214, 3215, 3216, 3217, 3218, 3219, 3220, 3221, 3223, 3224, 3225, 3226, 3227, 3228, 3229, 3230, 3231, 3232, 3233, 3235, 3236, 3237, 3238, 3239, 3240, 3241, 3242, 3243, 3244, 3245, 3247, 3248, 3250, 3251, 3252, 3253, 3254, 3255, 3256, 3257, 3259, 3260, 3261, 3262, 3263, 3265, 3266, 3267, 3268, 3269, 3271, 3272, 3273, 3274, 3275, 3279, 3280, 3281, 3283, 3284, 3285, 3287, 3289, 3290, 3291, 3292, 3293, 3295, 3296, 3297, 3298, 3299, 3300, 3301, 3302, 3303, 3304, 3305, 3307, 3308, 3309, 3310, 3313, 3314, 3315, 3316, 3317, 3319, 3320, 3321, 3322, 3323, 3324, 3325, 3326, 3327, 3328, 3329, 3331, 3333, 3334, 3335, 3338, 3339, 3340, 3341, 3342, 3343, 3344, 3345, 3346, 3347, 3348, 3349, 3351, 3352, 3353, 3354, 3355, 3356, 3357, 3358, 3359, 3361, 3362, 3363, 3364, 3365, 3367, 3368, 3369, 3370, 3371, 3372, 3373, 3374, 3375, 3376, 3377, 3379, 3380, 3381, 3382, 3383, 3384, 3385, 3386, 3387, 3389, 3391, 3392, 3393, 3394, 3395, 3396, 3397, 3398, 3399, 3400, 3401, 3402, 3403, 3404, 3405, 3406, 3407, 3409, 3410, 3411, 3412, 3413, 3414, 3415, 3416, 3417, 3418, 3419, 3420, 3421, 3422, 3423, 3424, 3425, 3426, 3427, 3428, 3429, 3431, 3433, 3434, 3435, 3436, 3437, 3438, 3439, 3440, 3441, 3442, 3443, 3445, 3446, 3447, 3448, 3449, 3451, 3452, 3453, 3454, 3455, 3457, 3458, 3459, 3460, 3461, 3463, 3464, 3465, 3466, 3467, 3468, 3469, 3470, 3471, 3473, 3475, 3476, 3477, 3478, 3479, 3481, 3482, 3483, 3484, 3485, 3487, 3488, 3489, 3490, 3491, 3493, 3494, 3495, 3496, 3497, 3499, 3501, 3502, 3503, 3504, 3505, 3506, 3507, 3508, 3509, 3511, 3512, 3513, 3514, 3515, 3517, 3518, 3519, 3520, 3521, 3523, 3524, 3525, 3526, 3527, 3529, 3530, 3531, 3532, 3533, 3535, 3536, 3537, 3538, 3539, 3540, 3541, 3542, 3543, 3544, 3545, 3546, 3547, 3548, 3549, 3550, 3551, 3553, 3554, 3555, 3557, 3559, 3560, 3561, 3562, 3563, 3565, 3566, 3567, 3568, 3569, 3571, 3572, 3573, 3574, 3576, 3577, 3578, 3579, 3580, 3581, 3583, 3584, 3585, 3586, 3587, 3589, 3590, 3591, 3592, 3593, 3595, 3597, 3598, 3599, 3600, 3601, 3602, 3603, 3604, 3605, 3607, 3609, 3610, 3611, 3613, 3614, 3615, 3616, 3617, 3619, 3620, 3621, 3622, 3623, 3625, 3626, 3627, 3628, 3629, 3631, 3632, 3633, 3634, 3635, 3637, 3638, 3639, 3641, 3643, 3644, 3645, 3646, 3647, 3648, 3649, 3650, 3651, 3652, 3653, 3655, 3656, 3657, 3658, 3659, 3661, 3662, 3663, 3664, 3665, 3666, 3667, 3668, 3669, 3670, 3671, 3673, 3674, 3675, 3676, 3677, 3679, 3680, 3681, 3682, 3683, 3684, 3685, 3686, 3687, 3688, 3689, 3691, 3692, 3694, 3695, 3697, 3698, 3699, 3700, 3701, 3703, 3704, 3705, 3706, 3707, 3708, 3709, 3710, 3711, 3713, 3715, 3716, 3717, 3718, 3719, 3721, 3722, 3723, 3724, 3725, 3727, 3728, 3729, 3730, 3731, 3733, 3734, 3735, 3736, 3737, 3739, 3740, 3741, 3742, 3743, 3745, 3747, 3748, 3749, 3751, 3752, 3753, 3754, 3755, 3756, 3757, 3758, 3759, 3760, 3761, 3763, 3764, 3765, 3766, 3767, 3769, 3771, 3772, 3773, 3775, 3776, 3777, 3778, 3779, 3781, 3782, 3783, 3784, 3785, 3787, 3788, 3789, 3791, 3792, 3793, 3794, 3795, 3797, 3799, 3800, 3801, 3802, 3803, 3804, 3805, 3806, 3807, 3808, 3809, 3811, 3812, 3813, 3814, 3815, 3817, 3818, 3819, 3820, 3821, 3823, 3824, 3825, 3826, 3827, 3829, 3830, 3831, 3832, 3833, 3835, 3837, 3838, 3839, 3841, 3842, 3843, 3844, 3845, 3847, 3848, 3849, 3851, 3852, 3853, 3854, 3855, 3856, 3857, 3859, 3860, 3861, 3862, 3863, 3865, 3866, 3867, 3868, 3869, 3871, 3872, 3873, 3874, 3875, 3877, 3878, 3879, 3880, 3881, 3883, 3884, 3885, 3886, 3887, 3889, 3890, 3891, 3893, 3895, 3896, 3897, 3898, 3901, 3902, 3903, 3904, 3905, 3907, 3908, 3909, 3910, 3911, 3913, 3914, 3915, 3916, 3917, 3919, 3920, 3921, 3922, 3923, 3924, 3925, 3926, 3927, 3928, 3929, 3931, 3932, 3933, 3934, 3935, 3937, 3939, 3940, 3941, 3943, 3945, 3946, 3947, 3949, 3950, 3951, 3953, 3955, 3956, 3957, 3958, 3959, 3961, 3962, 3963, 3964, 3965, 3967, 3968, 3969, 3970, 3971, 3972, 3973, 3974, 3975, 3977, 3979, 3980, 3981, 3982, 3983, 3985, 3986, 3987, 3988, 3989, 3991, 3992, 3993, 3994, 3995, 3996, 3997, 3998, 4000, 4001, 4003, 4005, 4006, 4007, 4009, 4010, 4011, 4012, 4013, 4015, 4017, 4018, 4019, 4021, 4022, 4023, 4024, 4025, 4027, 4028, 4029, 4030, 4031, 4033, 4034, 4035, 4036, 4037, 4038, 4039, 4040, 4041, 4042, 4043, 4044, 4045, 4046, 4047, 4048, 4049, 4050, 4051, 4052, 4053, 4054, 4055, 4056, 4057, 4058, 4059, 4061, 4062, 4063, 4064, 4065, 4066, 4067, 4069, 4070, 4071, 4072, 4073, 4074, 4075, 4076, 4077, 4078, 4079, 4081, 4082, 4083, 4084, 4085, 4087, 4089, 4090, 4091, 4093, 4094, 4095, 4096, 4097, 4099, 4101, 4102, 4103, 4104, 4105, 4106, 4109, 4111, 4112, 4113, 4114, 4115, 4117, 4119, 4120, 4121, 4123, 4124, 4125, 4126, 4127, 4129, 4130, 4131, 4132, 4133, 4135, 4136, 4137, 4138, 4139, 4142, 4143, 4145, 4147, 4148, 4149, 4150, 4151, 4153, 4154, 4155, 4157, 4159, 4160, 4161, 4162, 4163, 4164, 4165, 4166, 4167, 4168, 4169, 4171, 4173, 4174, 4175, 4176, 4177, 4178, 4179, 4181, 4183, 4184, 4185, 4186, 4187, 4188, 4189, 4190, 4191, 4192, 4193, 4194, 4195, 4196, 4197, 4198, 4199, 4201, 4202, 4203, 4204, 4205, 4207, 4209, 4210, 4211, 4212, 4213, 4214, 4215, 4216, 4217, 4219, 4220, 4221, 4222, 4223, 4225, 4226, 4227, 4229, 4231, 4232, 4233, 4234, 4235, 4237, 4238, 4239, 4240, 4241, 4243, 4244, 4245, 4246, 4247, 4248, 4249, 4250, 4251, 4252, 4253, 4254, 4255, 4256, 4257, 4258, 4259, 4260, 4261, 4262, 4263, 4264, 4265, 4266, 4267, 4268, 4269, 4270, 4271, 4273, 4274, 4275, 4276, 4277, 4279, 4280, 4281, 4282, 4283, 4285, 4286, 4287, 4288, 4289, 4291, 4292, 4293, 4294, 4295, 4297, 4298, 4299, 4300, 4301, 4303, 4304, 4305, 4306, 4307, 4308, 4309, 4310, 4311, 4312, 4313, 4315, 4316, 4318, 4319, 4321, 4322, 4323, 4324, 4325, 4327, 4328, 4329, 4330, 4331, 4332, 4333, 4334, 4335, 4336, 4337, 4338, 4339, 4340, 4341, 4342, 4343, 4345, 4346, 4347, 4348, 4349, 4351, 4352, 4353, 4354, 4355, 4356, 4357, 4358, 4359, 4360, 4361, 4363, 4364, 4365, 4366, 4367, 4368, 4369, 4370, 4371, 4373, 4375, 4376, 4377, 4378, 4379, 4381, 4382, 4383, 4384, 4385, 4387, 4388, 4389, 4390, 4391, 4393, 4394, 4395, 4397, 4398, 4399, 4400, 4401, 4402, 4403, 4405, 4406, 4407, 4408, 4409, 4410, 4411, 4412, 4413, 4414, 4415, 4417, 4418, 4419, 4420, 4421, 4423, 4424, 4425, 4426, 4427, 4429, 4430, 4431, 4432, 4433, 4435, 4436, 4437, 4438, 4439, 4441, 4442, 4443, 4444, 4445, 4447, 4449, 4450, 4451, 4453, 4454, 4455, 4456, 4457, 4459, 4460, 4461, 4462, 4463, 4465, 4466, 4467, 4468, 4469, 4471, 4472, 4473, 4474, 4475, 4476, 4477, 4478, 4479, 4480, 4481, 4483, 4484, 4485, 4486, 4487, 4489, 4490, 4491, 4492, 4493, 4495, 4496, 4497, 4498, 4499, 4501, 4502, 4503, 4504, 4505, 4507, 4509, 4510, 4511, 4513, 4514, 4515, 4516, 4517, 4519, 4521, 4523, 4524, 4525, 4526, 4527, 4528, 4529, 4531, 4532, 4533, 4534, 4536, 4537, 4538, 4539, 4540, 4541, 4543, 4544, 4545, 4546, 4547, 4548, 4549, 4550, 4551, 4552, 4553, 4555, 4556, 4557, 4558, 4559, 4561, 4562, 4563, 4565, 4567, 4568, 4569, 4570, 4571, 4572, 4573, 4574, 4575, 4576, 4577, 4579, 4581, 4582, 4583, 4585, 4586, 4587, 4588, 4589, 4591, 4592, 4593, 4594, 4595, 4596, 4597, 4598, 4599, 4600, 4601, 4603, 4604, 4605, 4606, 4607, 4608, 4609, 4610, 4611, 4612, 4613, 4615, 4616, 4617, 4618, 4619, 4621, 4622, 4623, 4624, 4625, 4627, 4628, 4629, 4630, 4631, 4633, 4634, 4635, 4637, 4639, 4641, 4642, 4643, 4645, 4646, 4647, 4649, 4651, 4652, 4653, 4654, 4655, 4656, 4657, 4658, 4659, 4660, 4661, 4663, 4665, 4666, 4667, 4669, 4670, 4671, 4672, 4673, 4675, 4676, 4677, 4678, 4679, 4681, 4682, 4683, 4684, 4685, 4687, 4688, 4689, 4690, 4691, 4693, 4694, 4695, 4696, 4697, 4699, 4700, 4701, 4702, 4703, 4705, 4706, 4707, 4708, 4709, 4711, 4712, 4713, 4715, 4718, 4719, 4721, 4723, 4724, 4725, 4726, 4727, 4729, 4730, 4731, 4732, 4733, 4735, 4737, 4738, 4740, 4741, 4742, 4743, 4744, 4745, 4747, 4748, 4749, 4750, 4751, 4753, 4754, 4755, 4756, 4757, 4759, 4760, 4761, 4762, 4764, 4765, 4766, 4767, 4768, 4769, 4771, 4772, 4773, 4774, 4777, 4779, 4780, 4781, 4783, 4784, 4785, 4786, 4787, 4789, 4791, 4793, 4795, 4796, 4797, 4799, 4801, 4802, 4803, 4804, 4805, 4807, 4808, 4809, 4810, 4811, 4813, 4814, 4815, 4816, 4817, 4819, 4820, 4821, 4822, 4823, 4824, 4825, 4826, 4827, 4828, 4829, 4831, 4832, 4833, 4834, 4835, 4836, 4837, 4838, 4839, 4841, 4843, 4844, 4845, 4846, 4847, 4849, 4850, 4851, 4852, 4853, 4855, 4856, 4857, 4858, 4859, 4861, 4862, 4863, 4864, 4865, 4867, 4868, 4869, 4870, 4871, 4872, 4873, 4874, 4875, 4876, 4877, 4879, 4880, 4881, 4882, 4883, 4884, 4885, 4886, 4887, 4888, 4889, 4891, 4892, 4893, 4894, 4895, 4898, 4899, 4900, 4901, 4903, 4904, 4905, 4906, 4907, 4908, 4909, 4910, 4911, 4913, 4915, 4916, 4917, 4918, 4919, 4921, 4922, 4923, 4924, 4925, 4927, 4928, 4929, 4931, 4932, 4933, 4934, 4935, 4936, 4937, 4939, 4940, 4941, 4942, 4943, 4944, 4945, 4946, 4947, 4948, 4949, 4951, 4952, 4953, 4955, 4957, 4958, 4959, 4960, 4961, 4963, 4964, 4965, 4966, 4967, 4968, 4969, 4970, 4971, 4972, 4973, 4975, 4976, 4977, 4978, 4979, 4981, 4982, 4983, 4985, 4987, 4988, 4989, 4990, 4991, 4993, 4994, 4995, 4996, 4997, 4999, 5000, 5001, 5002, 5003, 5005, 5006, 5007, 5008, 5009, 5011, 5013, 5014, 5015, 5017, 5018, 5019, 5021, 5023, 5025, 5026, 5027, 5029, 5030, 5031, 5032, 5033, 5035, 5036, 5037, 5038, 5039, 5041, 5042, 5043, 5045, 5047, 5048, 5049, 5050, 5051, 5052, 5053, 5054, 5055, 5057, 5059, 5060, 5061, 5062, 5063, 5065, 5066, 5067, 5069, 5070, 5071, 5072, 5073, 5074, 5075, 5077, 5079, 5081, 5083, 5084, 5085, 5086, 5087, 5089, 5090, 5091, 5093, 5095, 5096, 5097, 5098, 5099, 5100, 5101, 5102, 5103, 5105, 5107, 5108, 5109, 5110, 5111, 5112, 5113, 5114, 5115, 5116, 5117, 5119, 5120, 5121, 5122, 5123, 5125, 5126, 5127, 5128, 5129, 5131, 5132, 5133, 5134, 5135, 5137, 5138, 5139, 5140, 5141, 5142, 5143, 5144, 5145, 5146, 5147, 5149, 5151, 5152, 5153, 5154, 5155, 5156, 5157, 5159, 5161, 5162, 5163, 5165, 5166, 5167, 5168, 5169, 5170, 5171, 5172, 5173, 5174, 5175, 5176, 5177, 5179, 5181, 5182, 5183, 5184, 5185, 5186, 5187, 5188, 5189, 5191, 5192, 5193, 5194, 5195, 5196, 5197, 5198, 5199, 5200, 5201, 5202, 5203, 5204, 5205, 5206, 5207, 5209, 5210, 5211, 5212, 5213, 5215, 5216, 5217, 5218, 5219, 5221, 5222, 5223, 5224, 5225, 5227, 5228, 5229, 5230, 5231, 5233, 5235, 5237, 5239, 5240, 5241, 5242, 5245, 5246, 5247, 5248, 5249, 5251, 5252, 5253, 5254, 5255, 5257, 5258, 5259, 5260, 5261, 5263, 5264, 5265, 5266, 5267, 5269, 5270, 5271, 5272, 5273, 5275, 5276, 5277, 5278, 5279, 5281, 5282, 5283, 5284, 5285, 5287, 5288, 5289, 5291, 5293, 5294, 5295, 5296, 5297, 5299, 5300, 5301, 5302, 5303, 5305, 5306, 5307, 5308, 5309, 5311, 5312, 5313, 5315, 5316, 5317, 5318, 5319, 5320, 5321, 5322, 5323, 5324, 5325, 5326, 5327, 5328, 5329, 5330, 5331, 5332, 5333, 5334, 5335, 5336, 5337, 5338, 5339, 5341, 5342, 5343, 5344, 5345, 5346, 5347, 5349, 5350, 5351, 5353, 5354, 5355, 5356, 5357, 5358, 5359, 5360, 5361, 5362, 5363, 5365, 5366, 5367, 5369, 5371, 5372, 5373, 5374, 5375, 5377, 5378, 5379, 5381, 5383, 5384, 5385, 5386, 5387, 5389, 5390, 5391, 5392, 5393, 5395, 5396, 5397, 5398, 5399, 5401, 5402, 5403, 5405, 5407, 5408, 5409, 5410, 5411, 5412, 5413, 5414, 5415, 5416, 5417, 5419, 5420, 5421, 5422, 5423, 5424, 5425, 5427, 5428, 5429, 5431, 5433, 5434, 5435, 5437, 5438, 5439, 5440, 5441, 5443, 5444, 5445, 5446, 5447, 5449, 5450, 5451, 5452, 5453, 5455, 5457, 5458, 5459, 5461, 5462, 5463, 5464, 5465, 5467, 5469, 5470, 5471, 5472, 5473, 5474, 5475, 5476, 5477, 5479, 5481, 5482, 5483, 5484, 5485, 5486, 5487, 5488, 5489, 5491, 5492, 5493, 5494, 5495, 5497, 5498, 5499, 5500, 5501, 5503, 5504, 5505, 5506, 5507, 5509, 5511, 5512, 5513, 5515, 5516, 5517, 5518, 5519, 5521, 5522, 5523, 5524, 5525, 5527, 5528, 5529, 5530, 5531, 5533, 5534, 5535, 5537, 5539, 5540, 5541, 5542, 5543, 5544, 5545, 5546, 5547, 5549, 5551, 5553, 5554, 5555, 5557, 5558, 5559, 5561, 5563, 5565, 5566, 5567, 5569, 5570, 5571, 5572, 5573, 5575, 5576, 5577, 5578, 5579, 5580, 5581, 5582, 5583, 5584, 5585, 5587, 5589, 5590, 5591, 5593, 5594, 5595, 5596, 5597, 5599, 5600, 5601, 5602, 5604, 5606, 5607, 5608, 5609, 5611, 5612, 5613, 5614, 5615, 5616, 5617, 5618, 5619, 5620, 5621, 5623, 5624, 5625, 5626, 5627, 5628, 5629, 5631, 5632, 5633, 5635, 5636, 5637, 5638, 5639, 5641, 5642, 5643, 5644, 5645, 5647, 5648, 5649, 5650, 5651, 5652, 5653, 5654, 5655, 5656, 5657, 5659, 5660, 5661, 5662, 5663, 5665, 5666, 5667, 5668, 5669, 5671, 5672, 5673, 5675, 5677, 5678, 5679, 5681, 5683, 5684, 5685, 5686, 5687, 5689, 5690, 5691, 5692, 5693, 5695, 5696, 5697, 5698, 5699, 5700, 5701, 5702, 5703, 5705, 5707, 5708, 5709, 5710, 5711, 5713, 5714, 5715, 5716, 5717, 5719, 5721, 5723, 5725, 5726, 5727, 5728, 5729, 5731, 5732, 5733, 5734, 5735, 5737, 5738, 5739, 5741, 5743, 5744, 5745, 5746, 5747, 5749, 5750, 5751, 5752, 5753, 5755, 5756, 5757, 5758, 5759, 5761, 5762, 5763, 5764, 5765, 5767, 5768, 5769, 5770, 5771, 5772, 5773, 5774, 5775, 5776, 5777, 5779, 5780, 5781, 5782, 5783, 5785, 5786, 5787, 5788, 5789, 5791, 5793, 5794, 5795, 5797, 5798, 5799, 5800, 5801, 5803, 5804, 5805, 5806, 5807, 5809, 5810, 5811, 5812, 5813, 5815, 5817, 5819, 5821, 5822, 5823, 5824, 5825, 5827, 5828, 5829, 5830, 5831, 5832, 5833, 5834, 5835, 5836, 5837, 5839, 5841, 5842, 5843, 5845, 5846, 5847, 5848, 5849, 5851, 5853, 5857, 5858, 5859, 5860, 5861, 5863, 5864, 5865, 5866, 5867, 5868, 5869, 5871, 5873, 5875, 5876, 5877, 5878, 5879, 5881, 5882, 5883, 5884, 5885, 5887, 5888, 5889, 5891, 5892, 5893, 5894, 5895, 5897, 5899, 5901, 5902, 5903, 5905, 5906, 5907, 5909, 5911, 5912, 5913, 5915, 5917, 5918, 5919, 5920, 5921, 5923, 5924, 5925, 5926, 5927, 5929, 5930, 5931, 5932, 5933, 5935, 5936, 5937, 5938, 5939, 5941, 5943, 5944, 5945, 5947, 5948, 5949, 5950, 5951, 5952, 5953, 5954, 5955, 5956, 5957, 5959, 5961, 5962, 5963, 5965, 5966, 5967, 5968, 5969, 5971, 5972, 5973, 5974, 5975, 5976, 5977, 5978, 5979, 5980, 5981, 5983, 5984, 5985, 5986, 5987, 5988, 5989, 5990, 5991, 5992, 5993, 5995, 5996, 5997, 5998, 5999, 6000, 6001, 6002, 6003, 6004, 6005, 6007, 6008, 6009, 6010, 6011, 6012, 6013, 6014, 6015, 6016, 6017, 6019, 6021, 6022, 6023, 6025, 6026, 6027, 6029, 6031, 6032, 6033, 6034, 6035, 6037, 6038, 6039, 6040, 6041, 6043, 6044, 6045, 6046, 6047, 6048, 6049, 6050, 6051, 6052, 6053, 6054, 6055, 6057, 6059, 6061, 6062, 6063, 6064, 6065, 6066, 6067, 6069, 6070, 6071, 6073, 6075, 6077, 6079, 6081, 6082, 6083, 6084, 6085, 6086, 6087, 6088, 6089, 6091, 6092, 6093, 6094, 6095, 6096, 6097, 6100, 6101, 6103, 6104, 6105, 6106, 6107, 6109, 6110, 6111, 6112, 6113, 6115, 6117, 6118, 6119, 6120, 6121, 6122, 6124, 6125, 6127, 6128, 6129, 6130, 6131, 6133, 6134, 6135, 6136, 6137, 6139, 6141, 6142, 6143, 6144, 6146, 6147, 6148, 6149, 6151, 6152, 6153, 6154, 6155, 6156, 6157, 6158, 6159, 6161, 6162, 6163, 6164, 6165, 6166, 6167, 6169, 6171, 6173, 6175, 6176, 6177, 6178, 6179, 6181, 6182, 6183, 6185, 6187, 6189, 6190, 6191, 6193, 6194, 6195, 6197, 6199, 6201, 6202, 6203, 6205, 6206, 6207, 6208, 6209, 6211, 6212, 6213, 6214, 6215, 6216, 6217, 6218, 6219, 6220, 6221, 6223, 6224, 6225, 6226, 6227, 6229, 6230, 6231, 6233, 6235, 6236, 6237, 6238, 6239, 6241, 6243, 6245, 6247, 6248, 6249, 6251, 6253, 6254, 6255, 6256, 6257, 6259, 6260, 6261, 6262, 6263, 6265, 6266, 6267, 6268, 6269, 6271, 6272, 6273, 6274, 6275, 6277, 6278, 6279, 6281, 6283, 6285, 6286, 6287, 6289, 6290, 6291, 6292, 6293, 6295, 6296, 6297, 6298, 6299, 6301, 6302, 6303, 6305, 6307, 6308, 6309, 6310, 6311, 6312, 6313, 6314, 6315, 6316, 6317, 6319, 6320, 6321, 6322, 6323, 6324, 6325, 6326, 6327, 6329, 6331, 6332, 6333, 6334, 6335, 6336, 6337, 6339, 6340, 6341, 6343, 6345, 6346, 6347, 6349, 6350, 6351, 6352, 6353, 6354, 6355, 6356, 6357, 6358, 6359, 6361, 6362, 6363, 6365, 6367, 6369, 6370, 6371, 6373, 6374, 6375, 6376, 6377, 6379, 6380, 6381, 6382, 6383, 6384, 6385, 6386, 6387, 6389, 6391, 6392, 6393, 6394, 6395, 6397, 6398, 6399, 6400, 6401, 6403, 6404, 6405, 6406, 6407, 6409, 6410, 6411, 6412, 6413, 6415, 6416, 6417, 6418, 6419, 6421, 6422, 6423, 6425, 6427, 6428, 6429, 6430, 6431, 6433, 6434, 6435, 6436, 6437, 6439, 6441, 6442, 6443, 6445, 6446, 6447, 6449, 6451, 6452, 6453, 6454, 6455, 6456, 6457, 6458, 6459, 6460, 6461, 6463, 6464, 6465, 6466, 6467, 6468, 6469, 6470, 6471, 6472, 6473, 6475, 6476, 6477, 6478, 6479, 6481, 6483, 6484, 6485, 6487, 6488, 6489, 6490, 6491, 6493, 6494, 6495, 6497, 6498, 6499, 6501, 6502, 6503, 6505, 6506, 6507, 6508, 6509, 6511, 6512, 6513, 6514, 6515, 6516, 6517, 6518, 6519, 6521, 6523, 6525, 6526, 6527, 6529, 6530, 6531, 6533, 6535, 6536, 6537, 6538, 6539, 6540, 6541, 6542, 6543, 6544, 6545, 6547, 6548, 6549, 6550, 6551, 6553, 6554, 6555, 6556, 6557, 6559, 6560, 6561, 6562, 6563, 6565, 6566, 6567, 6568, 6569, 6571, 6572, 6573, 6574, 6575, 6577, 6578, 6579, 6581, 6583, 6584, 6585, 6586, 6587, 6588, 6589, 6591, 6592, 6593, 6595, 6596, 6597, 6598, 6599, 6601, 6602, 6603, 6605, 6606, 6607, 6608, 6609, 6610, 6611, 6613, 6614, 6615, 6616, 6617, 6619, 6620, 6621, 6622, 6623, 6625, 6626, 6627, 6628, 6629, 6631, 6633, 6634, 6635, 6637, 6638, 6639, 6640, 6641, 6643, 6644, 6645, 6646, 6647, 6649, 6650, 6651, 6652, 6653, 6655, 6657, 6659, 6661, 6662, 6664, 6665, 6667, 6668, 6669, 6670, 6671, 6673, 6674, 6675, 6677, 6679, 6681, 6682, 6683, 6684, 6685, 6686, 6687, 6689, 6691, 6693, 6695, 6697, 6698, 6699, 6701, 6703, 6704, 6705, 6706, 6707, 6708, 6709, 6710, 6711, 6712, 6713, 6715, 6716, 6717, 6718, 6719, 6721, 6722, 6723, 6724, 6725, 6727, 6728, 6729, 6730, 6731, 6733, 6734, 6735, 6736, 6737, 6739, 6740, 6741, 6742, 6743, 6745, 6746, 6747, 6749, 6751, 6753, 6754, 6755, 6757, 6758, 6759, 6760, 6761, 6763, 6764, 6765, 6766, 6767, 6769, 6770, 6771, 6772, 6773, 6775, 6776, 6777, 6778, 6779, 6781, 6782, 6783, 6785, 6787, 6788, 6789, 6790, 6791, 6793, 6794, 6795, 6797, 6799, 6800, 6801, 6802, 6803, 6805, 6806, 6807, 6809, 6811, 6812, 6813, 6814, 6815, 6816, 6817, 6818, 6819, 6820, 6821, 6823, 6824, 6825, 6826, 6827, 6829, 6830, 6831, 6833, 6835, 6836, 6837, 6838, 6839, 6840, 6841, 6842, 6843, 6844, 6845, 6847, 6848, 6849, 6850, 6851, 6852, 6853, 6854, 6855, 6856, 6857, 6858, 6859, 6861, 6862, 6863, 6864, 6865, 6866, 6867, 6868, 6869, 6871, 6873, 6874, 6875, 6877, 6878, 6879, 6880, 6881, 6883, 6884, 6885, 6886, 6887, 6889, 6890, 6891, 6892, 6893, 6895, 6897, 6898, 6899, 6900, 6901, 6903, 6905, 6907, 6909, 6910, 6911, 6912, 6913, 6914, 6915, 6917, 6919, 6920, 6921, 6922, 6923, 6924, 6925, 6926, 6927, 6928, 6929, 6931, 6932, 6933, 6934, 6935, 6937, 6939, 6941, 6943, 6944, 6945, 6946, 6947, 6949, 6950, 6951, 6952, 6953, 6954, 6955, 6956, 6957, 6958, 6959, 6961, 6962, 6963, 6964, 6965, 6967, 6968, 6969, 6970, 6971, 6973, 6974, 6975, 6976, 6977, 6979, 6980, 6981, 6982, 6983, 6985, 6987, 6988, 6989, 6991, 6992, 6993, 6994, 6995, 6997, 6998, 6999, 7000, 7001, 7003, 7004, 7005, 7007, 7009, 7010, 7011, 7012, 7013, 7015, 7016, 7017, 7018, 7019, 7021, 7022, 7023, 7024, 7027, 7029, 7030, 7031, 7033, 7034, 7035, 7036, 7037, 7039, 7041, 7042, 7043, 7045, 7046, 7047, 7048, 7049, 7051, 7052, 7053, 7054, 7055, 7056, 7057, 7058, 7059, 7061, 7063, 7065, 7066, 7067, 7068, 7069, 7070, 7071, 7072, 7073, 7075, 7076, 7077, 7078, 7079, 7081, 7082, 7083, 7085, 7087, 7089, 7090, 7091, 7093, 7094, 7095, 7096, 7097, 7099, 7100, 7101, 7102, 7103, 7104, 7105, 7107, 7108, 7109, 7111, 7112, 7113, 7114, 7115, 7116, 7117, 7118, 7119, 7121, 7123, 7124, 7125, 7126, 7127, 7129, 7131, 7132, 7133, 7135, 7136, 7137, 7138, 7139, 7141, 7142, 7143, 7145, 7147, 7150, 7151, 7153, 7154, 7155, 7156, 7157, 7159, 7160, 7161, 7162, 7163, 7164, 7165, 7166, 7167, 7168, 7169, 7171, 7173, 7174, 7175, 7176, 7177, 7178, 7179, 7181, 7183, 7185, 7187, 7189, 7190, 7191, 7193, 7195, 7196, 7197, 7198, 7199, 7200, 7201, 7202, 7203, 7204, 7205, 7207, 7209, 7210, 7211, 7213, 7214, 7215, 7217, 7219, 7220, 7221, 7222, 7223, 7226, 7229, 7231, 7232, 7233, 7234, 7235, 7236, 7237, 7238, 7239, 7241, 7243, 7244, 7245, 7246, 7247, 7248, 7249, 7250, 7251, 7252, 7253, 7255, 7257, 7258, 7259, 7261, 7262, 7263, 7264, 7265, 7267, 7269, 7270, 7271, 7273, 7275, 7276, 7277, 7278, 7279, 7280, 7282, 7283, 7284, 7285, 7286, 7287, 7288, 7289, 7290, 7291, 7292, 7293, 7295, 7297, 7298, 7299, 7300, 7301, 7303, 7304, 7305, 7306, 7307, 7309, 7310, 7311, 7312, 7313, 7315, 7316, 7317, 7318, 7319, 7321, 7322, 7323, 7324, 7325, 7327, 7328, 7329, 7330, 7331, 7333, 7334, 7335, 7336, 7337, 7339, 7340, 7341, 7342, 7343, 7345, 7346, 7347, 7348, 7349, 7351, 7353, 7354, 7355, 7357, 7358, 7359, 7361, 7363, 7365, 7366, 7367, 7369, 7370, 7371, 7373, 7375, 7376, 7377, 7378, 7379, 7381, 7382, 7383, 7385, 7387, 7389, 7390, 7391, 7393, 7394, 7395, 7397, 7399, 7400, 7401, 7402, 7405, 7406, 7407, 7408, 7409, 7411, 7413, 7414, 7415, 7417, 7419, 7421, 7423, 7424, 7425, 7426, 7427, 7428, 7429, 7430, 7431, 7432, 7433, 7435, 7437, 7438, 7439, 7441, 7442, 7443, 7444, 7445, 7447, 7448, 7449, 7451, 7452, 7453, 7454, 7455, 7456, 7457, 7459, 7460, 7461, 7462, 7463, 7465, 7466, 7467, 7468, 7469, 7471, 7472, 7473, 7474, 7475, 7476, 7477, 7478, 7479, 7480, 7481, 7483, 7484, 7485, 7486, 7487, 7488, 7489, 7491, 7492, 7493, 7495, 7496, 7497, 7498, 7499, 7500, 7501, 7502, 7503, 7505, 7507, 7508, 7509, 7510, 7511, 7512, 7513, 7515, 7517, 7519, 7521, 7522, 7523, 7525, 7526, 7528, 7529, 7531, 7533, 7535, 7536, 7537, 7538, 7539, 7541, 7544, 7545, 7546, 7547, 7548, 7549, 7550, 7551, 7552, 7553, 7555, 7557, 7558, 7559, 7561, 7562, 7563, 7564, 7565, 7567, 7568, 7569, 7571, 7573, 7574, 7575, 7576, 7577, 7579, 7580, 7581, 7582, 7583, 7585, 7589, 7591, 7592, 7593, 7594, 7595, 7597, 7598, 7599, 7601, 7603, 7604, 7605, 7606, 7607, 7608, 7609, 7610, 7611, 7612, 7613, 7615, 7616, 7617, 7618, 7619, 7621, 7622, 7623, 7624, 7625, 7626, 7627, 7628, 7629, 7630, 7631, 7633, 7634, 7635, 7636, 7637, 7639, 7640, 7641, 7642, 7643, 7645, 7646, 7647, 7648, 7649, 7650, 7651, 7652, 7653, 7654, 7655, 7657, 7658, 7659, 7660, 7661, 7663, 7665, 7667, 7669, 7671, 7672, 7673, 7675, 7677, 7678, 7679, 7681, 7682, 7683, 7685, 7687, 7688, 7689, 7691, 7693, 7695, 7697, 7699, 7700, 7701, 7702, 7703, 7705, 7706, 7707, 7708, 7709, 7711, 7713, 7714, 7715, 7716, 7717, 7718, 7719, 7720, 7721, 7723, 7724, 7725, 7726, 7727, 7729, 7730, 7731, 7733, 7734, 7735, 7737, 7738, 7739, 7741, 7742, 7743, 7744, 7745, 7746, 7747, 7748, 7749, 7750, 7751, 7753, 7755, 7757, 7758, 7759, 7760, 7761, 7762, 7763, 7765, 7766, 7767, 7768, 7769, 7771, 7772, 7773, 7774, 7775, 7777, 7779, 7781, 7783, 7784, 7785, 7786, 7787, 7789, 7790, 7791, 7792, 7793, 7795, 7797, 7798, 7799, 7801, 7802, 7803, 7804, 7805, 7807, 7809, 7810, 7811, 7813, 7814, 7815, 7816, 7817, 7819, 7821, 7822, 7823, 7825, 7826, 7827, 7829, 7831, 7832, 7833, 7834, 7835, 7836, 7837, 7838, 7839, 7840, 7841, 7843, 7845, 7846, 7847, 7849, 7850, 7851, 7853, 7855, 7857, 7858, 7859, 7861, 7862, 7863, 7865, 7867, 7869, 7870, 7871, 7873, 7874, 7875, 7876, 7877, 7879, 7881, 7882, 7883, 7884, 7886, 7887, 7888, 7889, 7891, 7892, 7893, 7894, 7895, 7896, 7897, 7898, 7899, 7900, 7901, 7903, 7904, 7905, 7906, 7907, 7909, 7910, 7911, 7912, 7913, 7914, 7915, 7916, 7917, 7918, 7919, 7921, 7925, 7926, 7927, 7928, 7929, 7931, 7932, 7933, 7934, 7935, 7937, 7938, 7939, 7941, 7942, 7943, 7945, 7946, 7947, 7948, 7949, 7951, 7952, 7953, 7954, 7955, 7957, 7958, 7959, 7961, 7963, 7964, 7965, 7966, 7967, 7969, 7970, 7971, 7972, 7973, 7975, 7976, 7977, 7978, 7979, 7981, 7983, 7985, 7987, 7988, 7989, 7990, 7991, 7993, 7994, 7995, 7996, 7997, 7999, 8000, 8001, 8003, 8005, 8006, 8007, 8008, 8009, 8011, 8012, 8013, 8014, 8017, 8018, 8019, 8021, 8023, 8025, 8027, 8029, 8030, 8031, 8033, 8035, 8036, 8037, 8038, 8039, 8041, 8042, 8043, 8044, 8045, 8047, 8048, 8049, 8050, 8051, 8053, 8055, 8057, 8059, 8060, 8061, 8062, 8063, 8065, 8066, 8067, 8069, 8071, 8072, 8073, 8074, 8075, 8077, 8078, 8079, 8081, 8083, 8085, 8086, 8087, 8089, 8090, 8091, 8093, 8095, 8097, 8098, 8099, 8100, 8101, 8102, 8103, 8105, 8106, 8107, 8108, 8109, 8110, 8111, 8113, 8115, 8116, 8117, 8119, 8121, 8122, 8123, 8125, 8126, 8127, 8129, 8131, 8132, 8133, 8134, 8137, 8138, 8139, 8140, 8141, 8143, 8145, 8146, 8147, 8149, 8150, 8151, 8153, 8155, 8156, 8157, 8158, 8159, 8161, 8162, 8163, 8165, 8167, 8168, 8169, 8171, 8173, 8174, 8175, 8177, 8179, 8180, 8181, 8182, 8183, 8185, 8186, 8187, 8188, 8189, 8191, 8192, 8193, 8194, 8195, 8197, 8198, 8199, 8200, 8201, 8202, 8203, 8205, 8206, 8207, 8209, 8210, 8211, 8212, 8213, 8214, 8215, 8217, 8218, 8219, 8220, 8221, 8222, 8223, 8224, 8225, 8227, 8228, 8229, 8230, 8231, 8233, 8234, 8235, 8236, 8237, 8239, 8241, 8242, 8243, 8244, 8245, 8246, 8247, 8248, 8249, 8251, 8253, 8254, 8255, 8257, 8258, 8259, 8261, 8263, 8264, 8265, 8266, 8267, 8268, 8269, 8270, 8271, 8272, 8273, 8275, 8276, 8277, 8278, 8279, 8281, 8282, 8283, 8284, 8285, 8287, 8289, 8290, 8291, 8292, 8293, 8294, 8295, 8296, 8297, 8299, 8301, 8302, 8303, 8305, 8307, 8308, 8309, 8311, 8312, 8313, 8314, 8315, 8317, 8318, 8319, 8321, 8323, 8325, 8327, 8329, 8330, 8331, 8332, 8333, 8335, 8336, 8337, 8338, 8339, 8341, 8342, 8343, 8345, 8347, 8348, 8349, 8351, 8353, 8355, 8356, 8357, 8359, 8361, 8362, 8363, 8365, 8366, 8367, 8368, 8369, 8371, 8373, 8374, 8375, 8377, 8378, 8379, 8380, 8381, 8383, 8384, 8385, 8386, 8387, 8389, 8390, 8391, 8392, 8393, 8395, 8397, 8398, 8399, 8400, 8401, 8402, 8403, 8404, 8405, 8407, 8409, 8411, 8413, 8414, 8415, 8417, 8419, 8420, 8421, 8422, 8423, 8425, 8426, 8428, 8429, 8431, 8433, 8434, 8435, 8436, 8437, 8438, 8439, 8441, 8443, 8444, 8445, 8446, 8447, 8449, 8450, 8451, 8452, 8453, 8455, 8457, 8458, 8459, 8461, 8462, 8463, 8464, 8465, 8467, 8468, 8469, 8471, 8473, 8474, 8475, 8478, 8479, 8481, 8482, 8483, 8485, 8486, 8487, 8488, 8489, 8491, 8492, 8493, 8494, 8495, 8497, 8498, 8499, 8500, 8501, 8502, 8503, 8504, 8505, 8506, 8507, 8508, 8509, 8510, 8511, 8513, 8515, 8516, 8517, 8518, 8519, 8521, 8522, 8523, 8524, 8525, 8527, 8529, 8530, 8531, 8533, 8534, 8535, 8536, 8537, 8539, 8541, 8542, 8543, 8546, 8547, 8548, 8549, 8551, 8552, 8553, 8554, 8555, 8556, 8557, 8558, 8559, 8560, 8561, 8563, 8564, 8565, 8566, 8567, 8569, 8570, 8571, 8572, 8573, 8575, 8577, 8578, 8579, 8581, 8582, 8583, 8585, 8587, 8589, 8590, 8591, 8594, 8595, 8597, 8599, 8601, 8602, 8603, 8605, 8606, 8607, 8608, 8609, 8611, 8612, 8613, 8614, 8615, 8616, 8617, 8618, 8619, 8620, 8621, 8623, 8625, 8626, 8627, 8629, 8630, 8631, 8633, 8635, 8636, 8637, 8638, 8639, 8641, 8642, 8643, 8644, 8645, 8647, 8649, 8651, 8653, 8654, 8655, 8656, 8657, 8659, 8660, 8661, 8662, 8663, 8665, 8666, 8667, 8668, 8669, 8670, 8671, 8672, 8673, 8674, 8675, 8677, 8678, 8679, 8681, 8683, 8685, 8687, 8689, 8690, 8691, 8693, 8695, 8696, 8697, 8698, 8699, 8700, 8701, 8702, 8703, 8704, 8705, 8707, 8709, 8710, 8711, 8712, 8713, 8714, 8715, 8716, 8717, 8719, 8721, 8722, 8723, 8724, 8725, 8726, 8727, 8728, 8729, 8731, 8733, 8734, 8735, 8737, 8738, 8739, 8740, 8741, 8743, 8745, 8746, 8747, 8749, 8750, 8751, 8752, 8753, 8755, 8756, 8757, 8758, 8759, 8761, 8762, 8763, 8765, 8767, 8768, 8769, 8770, 8771, 8773, 8774, 8775, 8777, 8779, 8781, 8782, 8783, 8786, 8787, 8789, 8791, 8792, 8793, 8794, 8795, 8797, 8798, 8799, 8800, 8801, 8803, 8804, 8805, 8806, 8807, 8809, 8810, 8811, 8812, 8813, 8815, 8817, 8818, 8819, 8821, 8822, 8823, 8825, 8827, 8828, 8829, 8830, 8831, 8833, 8834, 8835, 8836, 8837, 8839, 8840, 8841, 8842, 8843, 8845, 8846, 8847, 8849, 8851, 8852, 8853, 8854, 8855, 8857, 8858, 8859, 8860, 8861, 8863, 8865, 8866, 8867, 8868, 8869, 8870, 8871, 8873, 8875, 8877, 8878, 8879, 8881, 8882, 8883, 8884, 8885, 8887, 8888, 8889, 8891, 8892, 8893, 8894, 8895, 8896, 8897, 8899, 8900, 8901, 8902, 8903, 8905, 8906, 8907, 8908, 8909, 8911, 8912, 8913, 8914, 8915, 8916, 8917, 8918, 8919, 8920, 8921, 8923, 8925, 8926, 8927, 8928, 8929, 8931, 8933, 8935, 8936, 8937, 8938, 8939, 8940, 8941, 8943, 8945, 8947, 8948, 8949, 8950, 8951, 8953, 8954, 8955, 8956, 8957, 8959, 8960, 8961, 8962, 8963, 8965, 8966, 8967, 8968, 8969, 8971, 8972, 8973, 8974, 8975, 8977, 8978, 8979, 8980, 8981, 8982, 8983, 8984, 8985, 8986, 8987, 8989, 8990, 8991, 8992, 8993, 8995, 8997, 8998, 8999, 9001, 9002, 9003, 9004, 9005, 9007, 9009, 9010, 9011, 9012, 9013, 9014, 9015, 9016, 9017, 9019, 9020, 9021, 9022, 9023, 9025, 9026, 9027, 9029, 9031, 9032, 9033, 9037, 9039, 9040, 9041, 9043, 9045, 9046, 9047, 9049, 9050, 9051, 9053, 9055, 9056, 9057, 9058, 9059, 9060, 9061, 9062, 9063, 9065, 9067, 9069, 9071, 9072, 9073, 9074, 9075, 9076, 9077, 9079, 9080, 9081, 9082, 9083, 9084, 9085, 9086, 9087, 9089, 9090, 9091, 9092, 9093, 9094, 9095, 9097, 9098, 9099, 9101, 9103, 9104, 9105, 9106, 9107, 9109, 9111, 9112, 9113, 9115, 9117, 9118, 9119, 9121, 9123, 9124, 9125, 9127, 9128, 9129, 9130, 9131, 9133, 9134, 9135, 9137, 9139, 9141, 9142, 9143, 9145, 9146, 9147, 9148, 9149, 9151, 9153, 9154, 9155, 9157, 9158, 9159, 9161, 9163, 9164, 9165, 9166, 9167, 9169, 9170, 9171, 9172, 9173, 9175, 9177, 9178, 9179, 9181, 9182, 9183, 9184, 9185, 9187, 9188, 9189, 9190, 9191, 9193, 9194, 9195, 9197, 9199, 9201, 9202, 9203, 9205, 9206, 9207, 9208, 9209, 9211, 9213, 9214, 9215, 9216, 9217, 9218, 9219, 9220, 9221, 9223, 9224, 9225, 9226, 9227, 9229, 9231, 9233, 9235, 9236, 9237, 9238, 9239, 9241, 9242, 9243, 9245, 9247, 9248, 9249, 9250, 9251, 9253, 9254, 9255, 9257, 9259, 9260, 9261, 9262, 9263, 9264, 9265, 9266, 9267, 9269, 9271, 9272, 9273, 9275, 9276, 9277, 9278, 9279, 9281, 9283, 9284, 9285, 9286, 9287, 9289, 9291, 9293, 9295, 9297, 9298, 9300, 9301, 9303, 9304, 9305, 9307, 9308, 9309, 9310, 9311, 9313, 9314, 9315, 9316, 9317, 9319, 9321, 9323, 9325, 9326, 9327, 9328, 9329, 9331, 9333, 9334, 9335, 9337, 9338, 9339, 9340, 9341, 9343, 9345, 9346, 9347, 9349, 9350, 9351, 9353, 9355, 9356, 9357, 9358, 9359, 9361, 9362, 9363, 9364, 9365, 9367, 9368, 9369, 9371, 9373, 9374, 9375, 9376, 9377, 9379, 9381, 9382, 9383, 9385, 9386, 9387, 9388, 9389, 9391, 9392, 9393, 9394, 9395, 9397, 9398, 9399, 9401, 9403, 9405, 9406, 9407, 9408, 9409, 9410, 9411, 9413, 9415, 9416, 9417, 9418, 9419, 9421, 9422, 9423, 9425, 9427, 9428, 9429, 9430, 9431, 9432, 9433, 9434, 9435, 9437, 9439, 9441, 9442, 9443, 9444, 9445, 9446, 9447, 9448, 9449, 9451, 9452, 9453, 9454, 9455, 9457, 9458, 9459, 9460, 9461, 9463, 9465, 9467, 9469, 9470, 9471, 9472, 9473, 9475, 9476, 9477, 9478, 9479, 9481, 9482, 9483, 9485, 9487, 9488, 9489, 9491, 9493, 9494, 9495, 9497, 9499, 9500, 9501, 9502, 9503, 9504, 9505, 9506, 9507, 9508, 9509, 9511, 9512, 9513, 9514, 9515, 9516, 9517, 9518, 9519, 9520, 9521, 9522, 9523, 9524, 9525, 9527, 9528, 9529, 9530, 9531, 9532, 9533, 9535, 9536, 9537, 9538, 9539, 9541, 9543, 9544, 9545, 9546, 9547, 9549, 9551, 9552, 9553, 9555, 9556, 9557, 9559, 9560, 9561, 9562, 9563, 9565, 9566, 9567, 9568, 9569, 9571, 9573, 9575, 9577, 9579, 9580, 9581, 9583, 9584, 9585, 9586, 9587, 9589, 9590, 9591, 9593, 9595, 9596, 9597, 9598, 9599, 9600, 9601, 9602, 9603, 9604, 9605, 9607, 9608, 9609, 9610, 9611, 9613, 9615, 9616, 9617, 9619, 9621, 9622, 9623, 9624, 9625, 9626, 9627, 9628, 9629, 9631, 9632, 9633, 9634, 9635, 9637, 9638, 9639, 9640, 9641, 9643, 9645, 9646, 9647, 9648, 9649, 9650, 9651, 9652, 9655, 9657, 9658, 9659, 9661, 9662, 9663, 9664, 9665, 9667, 9668, 9669, 9671, 9673, 9674, 9675, 9676, 9677, 9679, 9681, 9682, 9685, 9686, 9687, 9688, 9689, 9691, 9693, 9694, 9695, 9697, 9698, 9700, 9701, 9703, 9704, 9705, 9706, 9707, 9709, 9710, 9711, 9713, 9715, 9717, 9718, 9719, 9721, 9722, 9723, 9724, 9725, 9727, 9729, 9730, 9731, 9732, 9733, 9734, 9735, 9736, 9737, 9739, 9740, 9741, 9742, 9743, 9744, 9745, 9746, 9747, 9748, 9749, 9751, 9752, 9753, 9754, 9755, 9756, 9757, 9758, 9759, 9760, 9761, 9763, 9764, 9765, 9766, 9767, 9769, 9770, 9771, 9773, 9775, 9776, 9777, 9778, 9779, 9781, 9783, 9785, 9787, 9788, 9789, 9790, 9791, 9792, 9793, 9794, 9795, 9797, 9799, 9800, 9801, 9802, 9803, 9804, 9805, 9806, 9807, 9808, 9809, 9811, 9813, 9814, 9815, 9817, 9819, 9820, 9821, 9823, 9824, 9825, 9826, 9827, 9829, 9830, 9831, 9832, 9833, 9835, 9837, 9838, 9839, 9841, 9842, 9843, 9845, 9847, 9849, 9850, 9851, 9853, 9854, 9855, 9857, 9859, 9860, 9861, 9862, 9863, 9864, 9865, 9866, 9867, 9868, 9869, 9871, 9872, 9873, 9874, 9875, 9876, 9877, 9878, 9879, 9881, 9883, 9885, 9886, 9887, 9889, 9890, 9891, 9892, 9893, 9895, 9896, 9897, 9898, 9899, 9901, 9903, 9904, 9905, 9907, 9908, 9909, 9910, 9911, 9913, 9914, 9915, 9917, 9919, 9920, 9922, 9923, 9925, 9926, 9927, 9929, 9931, 9932, 9933, 9934, 9935, 9937, 9938, 9939, 9940, 9941, 9943, 9944, 9945, 9946, 9947, 9948, 9949, 9951, 9952, 9953, 9955, 9956, 9957, 9959, 9961, 9963, 9964, 9965, 9967, 9968, 9969, 9970, 9971, 9972, 9973, 9974, 9975, 9976, 9977, 9978, 9979, 9981, 9982, 9983, 9984, 9985, 9986, 9987, 9988, 9989, 9990, 9991, 9992, 9993, 9994, 9995, 9998, 9999, 10000, 10001, 10003, 10004, 10005, 10006, 10007, 10009, 10011, 10013, 10015, 10016, 10017, 10019, 10021, 10023, 10024, 10025, 10027, 10028, 10029, 10030, 10033, 10034, 10035, 10037, 10039, 10041, 10043, 10045, 10046, 10047, 10049, 10051, 10053, 10054, 10055, 10056, 10057, 10058, 10059, 10060, 10061, 10063, 10064, 10065, 10066, 10067, 10069, 10071, 10072, 10073, 10074, 10075, 10077, 10078, 10079, 10081, 10082, 10083, 10085, 10087, 10089, 10090, 10091, 10093, 10095, 10097, 10099, 10101, 10102, 10103, 10105, 10106, 10107, 10109, 10111, 10112, 10113, 10114, 10115, 10117, 10118, 10119, 10121, 10123, 10125, 10126, 10129, 10130, 10131, 10132, 10133, 10135, 10137, 10138, 10139, 10141, 10142, 10143, 10144, 10145, 10147, 10148, 10149, 10150, 10151, 10153, 10155, 10156, 10157, 10159, 10161, 10162, 10163, 10165, 10166, 10167, 10168, 10169, 10171, 10172, 10173, 10174, 10175, 10177, 10179, 10180, 10181, 10183, 10184, 10185, 10186, 10187, 10189, 10191, 10192, 10193, 10195, 10196, 10197, 10198, 10199, 10201, 10203, 10204, 10205, 10207, 10209, 10210, 10211, 10213, 10214, 10215, 10216, 10217, 10219, 10221, 10222, 10223, 10225, 10226, 10227, 10228, 10229, 10231, 10232, 10233, 10234, 10236, 10237, 10238, 10239, 10240, 10241, 10242, 10243, 10245, 10246, 10247, 10249, 10250, 10251, 10253, 10255, 10256, 10257, 10259, 10261, 10262, 10263, 10265, 10267, 10268, 10269, 10270, 10271, 10272, 10273, 10274, 10275, 10277, 10279, 10280, 10281, 10282, 10283, 10285, 10287, 10288, 10289, 10291, 10292, 10293, 10295, 10297, 10298, 10299, 10300, 10301, 10303, 10304, 10305, 10306, 10307, 10308, 10309, 10310, 10311, 10313, 10315, 10316, 10317, 10318, 10319, 10321, 10322, 10323, 10325, 10327, 10329, 10330, 10331, 10333, 10334, 10335, 10336, 10337, 10339, 10340, 10341, 10342, 10343, 10345, 10346, 10347, 10349, 10351, 10352, 10353, 10354, 10355, 10356, 10357, 10358, 10359, 10360, 10361, 10363, 10365, 10366, 10367, 10368, 10369, 10370, 10371, 10372, 10373, 10375, 10376, 10377, 10378, 10379, 10380, 10381, 10383, 10385, 10387, 10388, 10389, 10390, 10391, 10393, 10394, 10395, 10396, 10397, 10399, 10400, 10401, 10402, 10403, 10404, 10405, 10406, 10407, 10409, 10411, 10412, 10413, 10414, 10415, 10417, 10418, 10419, 10420, 10421, 10423, 10425, 10426, 10427, 10429, 10430, 10431, 10432, 10433, 10435, 10436, 10437, 10438, 10439, 10440, 10441, 10442, 10443, 10445, 10447, 10448, 10449, 10450, 10451, 10453, 10454, 10455, 10456, 10457, 10459, 10460, 10461, 10463, 10465, 10467, 10468, 10469, 10471, 10472, 10473, 10474, 10475, 10476, 10477, 10478, 10479, 10481, 10482, 10483, 10484, 10485, 10487, 10489, 10491, 10493, 10494, 10495, 10496, 10497, 10498, 10499, 10501, 10502, 10503, 10504, 10505, 10507, 10508, 10509, 10510, 10511, 10512, 10513, 10515, 10517, 10518, 10519, 10521, 10522, 10523, 10524, 10525, 10526, 10527, 10529, 10530, 10531, 10532, 10533, 10534, 10535, 10537, 10538, 10539, 10540, 10541, 10543, 10545, 10546, 10547, 10549, 10550, 10551, 10552, 10553, 10555, 10557, 10558, 10559, 10560, 10561, 10562, 10563, 10565, 10567, 10568, 10569, 10570, 10571, 10573, 10574, 10575, 10576, 10577, 10579, 10580, 10581, 10582, 10583, 10585, 10586, 10587, 10588, 10589, 10591, 10593, 10594, 10595, 10597, 10598, 10599, 10601, 10603, 10604, 10605, 10606, 10607, 10609, 10610, 10611, 10613, 10615, 10616, 10617, 10618, 10619, 10621, 10622, 10623, 10625, 10627, 10628, 10629, 10630, 10631, 10633, 10634, 10635, 10637, 10638, 10639, 10641, 10642, 10643, 10645, 10646, 10647, 10649, 10651, 10652, 10653, 10654, 10655, 10657, 10658, 10659, 10660, 10661, 10663, 10664, 10665, 10666, 10667, 10669, 10670, 10671, 10672, 10673, 10675, 10677, 10679, 10681, 10683, 10685, 10687, 10689, 10690, 10691, 10693, 10694, 10695, 10696, 10697, 10699, 10701, 10702, 10703, 10705, 10707, 10708, 10709, 10711, 10712, 10714, 10715, 10716, 10717, 10718, 10719, 10720, 10721, 10723, 10725, 10726, 10727, 10729, 10730, 10731, 10733, 10735, 10737, 10738, 10739, 10741, 10743, 10745, 10747, 10749, 10750, 10751, 10753, 10754, 10755, 10756, 10757, 10759, 10760, 10761, 10762, 10763, 10765, 10766, 10767, 10768, 10769, 10771, 10772, 10773, 10774, 10775, 10777, 10778, 10779, 10781, 10783, 10784, 10785, 10786, 10787, 10788, 10789, 10790, 10791, 10793, 10795, 10797, 10798, 10799, 10801, 10802, 10803, 10805, 10807, 10809, 10810, 10811, 10813, 10814, 10815, 10816, 10817, 10819, 10821, 10823, 10825, 10826, 10827, 10829, 10831, 10832, 10833, 10834, 10835, 10837, 10838, 10839, 10841, 10843, 10844, 10845, 10846, 10847, 10849, 10850, 10851, 10852, 10853, 10855, 10857, 10858, 10859, 10861, 10862, 10863, 10865, 10867, 10869, 10870, 10871, 10873, 10874, 10875, 10877, 10879, 10881, 10882, 10883, 10884, 10885, 10886, 10887, 10889, 10891, 10893, 10894, 10895, 10897, 10898, 10899, 10900, 10901, 10903, 10904, 10905, 10906, 10907, 10908, 10909, 10910, 10911, 10913, 10915, 10916, 10917, 10918, 10919, 10921, 10922, 10923, 10924, 10925, 10927, 10929, 10930, 10931, 10933, 10934, 10935, 10936, 10937, 10939, 10941, 10942, 10943, 10945, 10946, 10947, 10949, 10951, 10952, 10953, 10955, 10957, 10958, 10959, 10960, 10961, 10963, 10964, 10965, 10966, 10967, 10969, 10970, 10971, 10972, 10973, 10975, 10977, 10978, 10979, 10981, 10982, 10983, 10984, 10985, 10987, 10989, 10991, 10993, 10994, 10995, 10996, 10997, 10999, 11001, 11002, 11003, 11005, 11006, 11007, 11008, 11009, 11011, 11012, 11013, 11015, 11017, 11018, 11019, 11021, 11023, 11024, 11027, 11028, 11029, 11030, 11031, 11032, 11033, 11035, 11036, 11037, 11038, 11039, 11041, 11042, 11043, 11045, 11047, 11048, 11049, 11050, 11051, 11053, 11054, 11055, 11056, 11057, 11059, 11061, 11062, 11063, 11065, 11066, 11067, 11068, 11069, 11071, 11073, 11074, 11075, 11077, 11078, 11079, 11081, 11083, 11084, 11085, 11087, 11089, 11091, 11093, 11095, 11097, 11098, 11099, 11101, 11102, 11103, 11105, 11106, 11107, 11108, 11109, 11111, 11113, 11115, 11117, 11119, 11121, 11122, 11123, 11124, 11125, 11126, 11127, 11128, 11129, 11131, 11133, 11134, 11135, 11137, 11138, 11139, 11140, 11141, 11143, 11145, 11146, 11147, 11149, 11150, 11151, 11152, 11153, 11155, 11156, 11157, 11158, 11159, 11161, 11162, 11163, 11164, 11165, 11167, 11168, 11169, 11170, 11171, 11173, 11174, 11175, 11176, 11177, 11178, 11179, 11181, 11182, 11183, 11185, 11187, 11188, 11189, 11191, 11192, 11193, 11194, 11195, 11197, 11198, 11199, 11201, 11203, 11205, 11207, 11209, 11210, 11211, 11213, 11215, 11216, 11217, 11218, 11219, 11221, 11223, 11226, 11227, 11229, 11230, 11231, 11233, 11234, 11235, 11236, 11237, 11238, 11239, 11240, 11241, 11243, 11245, 11246, 11247, 11248, 11249, 11250, 11251, 11252, 11253, 11254, 11255, 11257, 11258, 11259, 11261, 11263, 11265, 11266, 11267, 11268, 11269, 11270, 11271, 11272, 11273, 11275, 11276, 11277, 11278, 11279, 11281, 11283, 11285, 11287, 11288, 11289, 11290, 11291, 11293, 11294, 11295, 11296, 11297, 11299, 11300, 11301, 11302, 11303, 11305, 11306, 11307, 11309, 11311, 11313, 11314, 11315, 11317, 11318, 11319, 11321, 11323, 11324, 11325, 11327, 11328, 11329, 11330, 11331, 11332, 11333, 11335, 11337, 11338, 11339, 11341, 11342, 11343, 11344, 11345, 11347, 11348, 11349, 11350, 11351, 11353, 11354, 11355, 11357, 11359, 11361, 11362, 11363, 11365, 11366, 11367, 11368, 11369, 11371, 11372, 11373, 11375, 11377, 11378, 11379, 11381, 11383, 11384, 11385, 11386, 11387, 11389, 11390, 11391, 11392, 11393, 11395, 11396, 11397, 11399, 11401, 11403, 11404, 11405, 11407, 11409, 11410, 11411, 11413, 11414, 11415, 11416, 11417, 11419, 11420, 11421, 11422, 11423, 11425, 11426, 11427, 11428, 11429, 11431, 11433, 11435, 11436, 11437, 11438, 11439, 11440, 11441, 11443, 11444, 11445, 11446, 11447, 11449, 11451, 11453, 11455, 11456, 11457, 11458, 11459, 11461, 11462, 11463, 11464, 11465, 11467, 11469, 11470, 11471, 11472, 11473, 11475, 11476, 11477, 11479, 11481, 11482, 11483, 11485, 11486, 11487, 11488, 11489, 11491, 11492, 11493, 11494, 11495, 11497, 11498, 11499, 11500, 11501, 11503, 11504, 11505, 11506, 11507, 11509, 11510, 11511, 11513, 11515, 11516, 11517, 11519, 11521, 11522, 11523, 11525, 11527, 11528, 11529, 11530, 11531, 11533, 11534, 11535, 11537, 11539, 11541, 11542, 11543, 11544, 11545, 11546, 11547, 11548, 11549, 11551, 11552, 11553, 11554, 11555, 11557, 11558, 11559, 11560, 11561, 11563, 11565, 11566, 11567, 11569, 11571, 11572, 11573, 11575, 11576, 11577, 11578, 11579, 11581, 11582, 11583, 11584, 11585, 11587, 11588, 11589, 11590, 11591, 11593, 11594, 11595, 11596, 11597, 11599, 11600, 11601, 11602, 11603, 11604, 11605, 11606, 11607, 11608, 11609, 11611, 11612, 11613, 11614, 11615, 11617, 11618, 11619, 11621, 11623, 11624, 11625, 11627, 11629, 11631, 11632, 11633, 11635, 11636, 11637, 11638, 11639, 11641, 11642, 11643, 11644, 11645, 11647, 11648, 11649, 11650, 11651, 11653, 11654, 11655, 11656, 11657, 11659, 11660, 11661, 11662, 11663, 11664, 11665, 11666, 11667, 11668, 11669, 11671, 11672, 11673, 11674, 11675, 11677, 11678, 11679, 11681, 11683, 11684, 11685, 11686, 11687, 11689, 11690, 11691, 11693, 11695, 11697, 11699, 11701, 11703, 11705, 11707, 11709, 11710, 11711, 11712, 11713, 11714, 11715, 11716, 11717, 11719, 11720, 11721, 11722, 11723, 11725, 11726, 11727, 11729, 11731, 11733, 11735, 11737, 11739, 11741, 11743, 11744, 11745, 11746, 11747, 11749, 11750, 11751, 11752, 11753, 11755, 11757, 11758, 11759, 11760, 11761, 11762, 11763, 11765, 11767, 11769, 11770, 11771, 11773, 11774, 11775, 11776, 11777, 11779, 11781, 11782, 11783, 11785, 11786, 11787, 11789, 11791, 11793, 11795, 11796, 11797, 11798, 11799, 11801, 11803, 11804, 11805, 11806, 11807, 11809, 11811, 11812, 11813, 11815, 11817, 11819, 11821, 11822, 11823, 11825, 11827, 11828, 11829, 11830, 11831, 11833, 11834, 11835, 11836, 11837, 11839, 11841, 11843, 11845, 11846, 11847, 11849, 11851, 11852, 11853, 11854, 11855, 11857, 11858, 11859, 11861, 11863, 11864, 11865, 11866, 11867, 11869, 11870, 11871, 11873, 11875, 11877, 11879, 11881, 11882, 11883, 11884, 11885, 11887, 11888, 11889, 11890, 11891, 11892, 11893, 11894, 11895, 11897, 11899, 11901, 11902, 11903, 11904, 11906, 11907, 11909, 11911, 11912, 11913, 11914, 11915, 11916, 11917, 11918, 11919, 11920, 11923, 11924, 11925, 11926, 11927, 11929, 11930, 11931, 11933, 11935, 11937, 11938, 11939, 11940, 11941, 11942, 11943, 11945, 11947, 11948, 11949, 11950, 11951, 11953, 11954, 11955, 11957, 11959, 11960, 11961, 11962, 11964, 11965, 11967, 11968, 11969, 11971, 11973, 11974, 11975, 11977, 11978, 11979, 11980, 11981, 11983, 11984, 11985, 11987, 11988, 11989, 11990, 11991, 11992, 11993, 11995, 11997, 11998, 12000, 12001, 12002, 12003, 12004, 12005, 12007, 12008, 12009, 12010, 12011, 12013, 12014, 12015, 12016, 12017, 12019, 12020, 12021, 12022, 12023, 12024, 12025, 12026, 12027, 12029, 12031, 12033, 12035, 12037, 12039, 12040, 12041, 12043, 12044, 12045, 12046, 12047, 12049, 12050, 12051, 12053, 12055, 12056, 12057, 12058, 12059, 12061, 12062, 12063, 12064, 12065, 12067, 12069, 12070, 12071, 12072, 12073, 12074, 12075, 12077, 12079, 12080, 12081, 12082, 12083, 12085, 12086, 12087, 12089, 12091, 12092, 12093, 12094, 12096, 12097, 12098, 12099, 12100, 12101, 12103, 12104, 12105, 12107, 12109, 12110, 12111, 12112, 12113, 12115, 12116, 12117, 12118, 12119, 12121, 12122, 12123, 12125, 12127, 12128, 12129, 12130, 12131, 12132, 12133, 12134, 12135, 12136, 12137, 12139, 12140, 12141, 12143, 12145, 12147, 12148, 12149, 12151, 12152, 12153, 12154, 12155, 12157, 12158, 12159, 12161, 12163, 12164, 12165, 12166, 12167, 12168, 12169, 12170, 12171, 12172, 12173, 12175, 12176, 12177, 12178, 12179, 12181, 12182, 12183, 12185, 12187, 12188, 12189, 12190, 12191, 12193, 12194, 12195, 12196, 12197, 12198, 12199, 12200, 12201, 12202, 12203, 12205, 12206, 12207, 12209, 12211, 12212, 12213, 12214, 12215, 12217, 12218, 12219, 12220, 12221, 12223, 12225, 12227, 12229, 12230, 12231, 12232, 12233, 12235, 12237, 12238, 12239, 12241, 12242, 12243, 12244, 12245, 12247, 12249, 12251, 12253, 12254, 12255, 12257, 12259, 12260, 12261, 12262, 12263, 12265, 12266, 12267, 12268, 12269, 12271, 12272, 12273, 12275, 12276, 12277, 12278, 12279, 12281, 12283, 12284, 12286, 12287, 12289, 12290, 12291, 12293, 12295, 12296, 12297, 12298, 12299, 12301, 12302, 12303, 12304, 12305, 12307, 12309, 12310, 12311, 12312, 12313, 12315, 12317, 12318, 12319, 12322, 12323, 12324, 12325, 12326, 12327, 12328, 12329, 12330, 12331, 12333, 12334, 12335, 12337, 12338, 12339, 12340, 12341, 12343, 12344, 12345, 12346, 12347, 12349, 12350, 12351, 12352, 12353, 12355, 12357, 12358, 12359, 12361, 12362, 12363, 12364, 12365, 12367, 12369, 12370, 12371, 12373, 12374, 12375, 12377, 12379, 12381, 12382, 12383, 12384, 12385, 12386, 12387, 12389, 12391, 12392, 12395, 12396, 12397, 12398, 12399, 12401, 12403, 12405, 12406, 12407, 12409, 12410, 12411, 12412, 12413, 12415, 12416, 12417, 12418, 12419, 12421, 12422, 12423, 12424, 12425, 12427, 12429, 12430, 12431, 12432, 12433, 12434, 12435, 12436, 12437, 12439, 12441, 12442, 12444, 12445, 12446, 12447, 12448, 12449, 12451, 12452, 12453, 12454, 12455, 12457, 12459, 12461, 12463, 12464, 12465, 12466, 12467, 12468, 12469, 12470, 12471, 12473, 12477, 12478, 12479, 12481, 12482, 12483, 12485, 12487, 12488, 12489, 12491, 12493, 12495, 12497, 12499, 12500, 12501, 12502, 12503, 12505, 12506, 12507, 12508, 12509, 12511, 12513, 12514, 12515, 12517, 12519, 12521, 12523, 12525, 12526, 12527, 12529, 12531, 12533, 12535, 12536, 12537, 12538, 12539, 12541, 12542, 12543, 12544, 12545, 12547, 12548, 12549, 12550, 12551, 12553, 12555, 12556, 12557, 12559, 12561, 12562, 12563, 12564, 12565, 12566, 12567, 12568, 12569, 12571, 12573, 12574, 12575, 12577, 12578, 12579, 12581, 12583, 12585, 12586, 12587, 12589, 12590, 12591, 12592, 12593, 12595, 12597, 12598, 12599, 12601, 12603, 12604, 12605, 12607, 12608, 12609, 12610, 12611, 12613, 12614, 12615, 12617, 12619, 12620, 12621, 12622, 12623, 12625, 12626, 12627, 12629, 12631, 12632, 12633, 12634, 12635, 12637, 12638, 12639, 12641, 12643, 12644, 12645, 12646, 12647, 12649, 12651, 12653, 12655, 12656, 12657, 12658, 12659, 12661, 12662, 12663, 12665, 12667, 12668, 12669, 12671, 12673, 12674, 12675, 12676, 12677, 12679, 12681, 12683, 12684, 12685, 12686, 12687, 12689, 12691, 12693, 12695, 12697, 12698, 12699, 12700, 12701, 12703, 12704, 12705, 12706, 12707, 12709, 12710, 12711, 12713, 12715, 12716, 12717, 12719, 12721, 12723, 12725, 12727, 12728, 12729, 12730, 12731, 12732, 12733, 12734, 12735, 12737, 12739, 12740, 12741, 12743, 12745, 12746, 12747, 12748, 12749, 12751, 12753, 12754, 12755, 12756, 12757, 12758, 12759, 12760, 12761, 12763, 12764, 12765, 12766, 12767, 12769, 12770, 12771, 12772, 12773, 12775, 12776, 12777, 12778, 12779, 12781, 12783, 12784, 12785, 12787, 12789, 12790, 12791, 12793, 12794, 12795, 12797, 12799, 12800, 12801, 12802, 12803, 12805, 12806, 12807, 12809, 12811, 12812, 12813, 12815, 12817, 12818, 12819, 12820, 12821, 12823, 12824, 12825, 12827, 12829, 12830, 12831, 12833, 12835, 12836, 12837, 12838, 12839, 12841, 12843, 12844, 12845, 12847, 12849, 12851, 12853, 12854, 12855, 12857, 12859, 12861, 12863, 12865, 12866, 12867, 12868, 12869, 12871, 12872, 12873, 12874, 12875, 12876, 12877, 12878, 12879, 12880, 12881, 12883, 12885, 12886, 12887, 12889, 12890, 12891, 12892, 12893, 12895, 12896, 12897, 12898, 12899, 12900, 12901, 12902, 12903, 12904, 12905, 12907, 12909, 12910, 12911, 12913, 12914, 12915, 12916, 12917, 12919, 12921, 12922, 12923, 12925, 12926, 12927, 12928, 12929, 12931, 12932, 12933, 12934, 12935, 12937, 12938, 12939, 12940, 12941, 12942, 12943, 12944, 12945, 12946, 12947, 12948, 12949, 12951, 12952, 12953, 12955, 12957, 12958, 12959, 12961, 12962, 12963, 12965, 12967, 12968, 12969, 12970, 12971, 12973, 12975, 12976, 12977, 12979, 12981, 12982, 12983, 12984, 12985, 12986, 12987, 12989, 12991, 12992, 12993, 12995, 12996, 12997, 12998, 12999, 13001, 13003, 13004, 13005, 13006, 13007, 13008, 13009, 13010, 13011, 13012, 13013, 13015, 13016, 13017, 13018, 13019, 13021, 13022, 13023, 13024, 13025, 13027, 13028, 13029, 13031, 13033, 13034, 13035, 13037, 13039, 13040, 13041, 13043, 13045, 13046, 13047, 13049, 13050, 13051, 13052, 13053, 13054, 13057, 13059, 13060, 13061, 13063, 13065, 13066, 13067, 13068, 13069, 13070, 13071, 13072, 13073, 13075, 13076, 13077, 13078, 13079, 13081, 13082, 13083, 13084, 13085, 13087, 13089, 13090, 13091, 13092, 13093, 13094, 13095, 13097, 13099, 13101, 13102, 13103, 13105, 13106, 13107, 13108, 13109, 13111, 13113, 13114, 13115, 13117, 13118, 13119, 13121, 13122, 13123, 13125, 13126, 13127, 13129, 13130, 13131, 13132, 13133, 13135, 13136, 13137, 13138, 13139, 13141, 13142, 13143, 13144, 13145, 13147, 13149, 13151, 13153, 13155, 13157, 13159, 13161, 13162, 13163, 13165, 13166, 13167, 13169, 13171, 13172, 13173, 13174, 13175, 13176, 13177, 13178, 13179, 13180, 13181, 13183, 13184, 13185, 13187, 13190, 13191, 13192, 13193, 13195, 13196, 13197, 13198, 13199, 13201, 13203, 13204, 13205, 13207, 13208, 13209, 13210, 13211, 13212, 13213, 13214, 13215, 13217, 13219, 13220, 13222, 13223, 13224, 13226, 13227, 13229, 13231, 13233, 13234, 13235, 13237, 13238, 13239, 13241, 13243, 13245, 13247, 13249, 13250, 13251, 13252, 13253, 13255, 13256, 13257, 13258, 13259, 13261, 13262, 13263, 13264, 13265, 13267, 13268, 13269, 13270, 13271, 13273, 13274, 13275, 13276, 13277, 13281, 13283, 13285, 13287, 13289, 13291, 13292, 13293, 13294, 13295, 13297, 13298, 13299, 13301, 13303, 13304, 13305, 13307, 13309, 13311, 13313, 13315, 13316, 13317, 13318, 13319, 13321, 13322, 13323, 13324, 13325, 13327, 13328, 13329, 13330, 13331, 13333, 13335, 13336, 13337, 13339, 13340, 13341, 13343, 13344, 13345, 13347, 13348, 13349, 13351, 13353, 13354, 13355, 13357, 13358, 13359, 13361, 13363, 13364, 13365, 13366, 13367, 13369, 13370, 13371, 13373, 13375, 13376, 13377, 13379, 13381, 13383, 13384, 13385, 13387, 13389, 13390, 13391, 13393, 13394, 13395, 13396, 13397, 13399, 13401, 13402, 13403, 13404, 13405, 13406, 13407, 13408, 13409, 13411, 13413, 13415, 13417, 13418, 13419, 13421, 13422, 13423, 13425, 13426, 13427, 13428, 13429, 13431, 13432, 13433, 13434, 13435, 13437, 13438, 13439, 13441, 13442, 13443, 13444, 13445, 13446, 13447, 13448, 13449, 13450, 13451, 13454, 13455, 13456, 13457, 13459, 13460, 13461, 13463, 13465, 13466, 13467, 13469, 13471, 13472, 13473, 13474, 13475, 13476, 13477, 13479, 13481, 13483, 13485, 13486, 13487, 13489, 13490, 13491, 13492, 13493, 13495, 13497, 13498, 13499, 13501, 13502, 13503, 13505, 13507, 13508, 13509, 13511, 13513, 13514, 13515, 13516, 13517, 13519, 13520, 13521, 13522, 13523, 13527, 13528, 13529, 13531, 13532, 13533, 13535, 13537, 13538, 13539, 13540, 13541, 13543, 13544, 13545, 13546, 13547, 13548, 13549, 13550, 13551, 13552, 13553, 13555, 13556, 13557, 13558, 13559, 13561, 13563, 13564, 13565, 13567, 13568, 13569, 13570, 13571, 13573, 13574, 13575, 13576, 13577, 13579, 13581, 13582, 13583, 13584, 13585, 13589, 13591, 13593, 13594, 13597, 13599, 13601, 13603, 13604, 13605, 13606, 13607, 13609, 13610, 13611, 13612, 13613, 13615, 13616, 13617, 13618, 13619, 13620, 13621, 13622, 13623, 13625, 13627, 13628, 13629, 13630, 13631, 13633, 13634, 13635, 13637, 13639, 13641, 13642, 13643, 13644, 13645, 13646, 13647, 13649, 13651, 13652, 13653, 13654, 13655, 13657, 13659, 13661, 13663, 13665, 13666, 13667, 13669, 13671, 13672, 13673, 13675, 13676, 13677, 13678, 13679, 13681, 13682, 13683, 13685, 13687, 13690, 13691, 13693, 13694, 13695, 13696, 13697, 13699, 13700, 13701, 13703, 13705, 13706, 13707, 13709, 13711, 13712, 13713, 13715, 13716, 13717, 13719, 13720, 13721, 13722, 13723, 13724, 13725, 13726, 13727, 13729, 13730, 13731, 13732, 13733, 13734, 13735, 13737, 13739, 13741, 13742, 13743, 13745, 13747, 13749, 13750, 13751, 13753, 13754, 13755, 13757, 13759, 13760, 13761, 13762, 13763, 13764, 13765, 13766, 13767, 13768, 13769, 13771, 13772, 13773, 13774, 13775, 13777, 13778, 13779, 13780, 13781, 13783, 13785, 13787, 13789, 13790, 13791, 13793, 13795, 13796, 13797, 13799, 13801, 13802, 13803, 13805, 13806, 13807, 13808, 13809, 13810, 13811, 13813, 13814, 13815, 13817, 13819, 13821, 13822, 13823, 13825, 13826, 13827, 13828, 13829, 13831, 13832, 13834, 13835, 13836, 13837, 13838, 13840, 13841, 13842, 13843, 13844, 13845, 13846, 13847, 13849, 13850, 13851, 13852, 13853, 13855, 13856, 13857, 13859, 13861, 13862, 13863, 13865, 13867, 13869, 13870, 13871, 13872, 13873, 13874, 13875, 13876, 13877, 13879, 13881, 13882, 13883, 13885, 13886, 13887, 13889, 13891, 13892, 13893, 13894, 13895, 13897, 13898, 13899, 13900, 13901, 13903, 13905, 13906, 13907, 13909, 13911, 13912, 13913, 13915, 13917, 13918, 13919, 13921, 13922, 13924, 13925, 13927, 13928, 13929, 13930, 13931, 13932, 13933, 13934, 13935, 13937, 13939, 13941, 13942, 13943, 13945, 13946, 13947, 13948, 13949, 13951, 13952, 13953, 13954, 13955, 13956, 13957, 13958, 13959, 13961, 13963, 13965, 13967, 13968, 13969, 13970, 13971, 13973, 13975, 13976, 13977, 13978, 13979, 13981, 13982, 13983, 13985, 13987, 13989, 13990, 13991, 13993, 13994, 13995, 13996, 13997, 13999, 14000, 14001, 14002, 14003, 14005, 14006, 14007, 14009, 14011, 14013, 14014, 14015, 14017, 14018, 14019, 14020, 14021, 14024, 14025, 14026, 14027, 14029, 14030, 14031, 14033, 14035, 14036, 14037, 14038, 14039, 14041, 14043, 14044, 14045, 14047, 14048, 14049, 14050, 14051, 14052, 14053, 14054, 14055, 14057, 14059, 14060, 14061, 14062, 14063, 14066, 14067, 14068, 14069, 14071, 14073, 14074, 14075, 14076, 14077, 14078, 14079, 14080, 14081, 14083, 14084, 14085, 14086, 14087, 14089, 14090, 14091, 14092, 14093, 14095, 14097, 14098, 14099, 14101, 14102, 14103, 14104, 14105, 14107, 14108, 14109, 14110, 14111, 14112, 14113, 14115, 14116, 14117, 14119, 14120, 14121, 14123, 14125, 14126, 14127, 14128, 14129, 14131, 14132, 14133, 14135, 14137, 14138, 14139, 14140, 14141, 14143, 14144, 14145, 14147, 14149, 14150, 14151, 14153, 14155, 14157, 14158, 14159, 14161, 14162, 14163, 14164, 14165, 14166, 14167, 14169, 14170, 14171, 14173, 14174, 14175, 14176, 14177, 14179, 14181, 14183, 14185, 14186, 14187, 14189, 14191, 14192, 14193, 14195, 14197, 14198, 14199, 14201, 14203, 14204, 14205, 14207, 14208, 14209, 14210, 14211, 14213, 14215, 14216, 14217, 14218, 14219, 14221, 14222, 14223, 14225, 14227, 14229, 14231, 14233, 14234, 14235, 14237, 14239, 14241, 14242, 14243, 14244, 14245, 14246, 14247, 14248, 14249, 14251, 14252, 14253, 14255, 14257, 14258, 14259, 14260, 14261, 14263, 14265, 14266, 14267, 14269, 14271, 14272, 14273, 14275, 14276, 14278, 14279, 14281, 14282, 14283, 14284, 14287, 14289, 14291, 14292, 14293, 14294, 14295, 14297, 14299, 14300, 14301, 14302, 14303, 14305, 14306, 14307, 14308, 14309, 14311, 14312, 14313, 14314, 14315, 14317, 14318, 14319, 14321, 14323, 14324, 14325, 14326, 14327, 14329, 14330, 14331, 14332, 14333, 14335, 14336, 14337, 14339, 14341, 14343, 14344, 14345, 14347, 14348, 14349, 14351, 14352, 14353, 14355, 14356, 14357, 14359, 14361, 14362, 14363, 14365, 14366, 14367, 14368, 14369, 14371, 14372, 14373, 14374, 14375, 14377, 14378, 14379, 14380, 14381, 14383, 14385, 14386, 14387, 14389, 14390, 14391, 14392, 14393, 14395, 14396, 14397, 14398, 14399, 14400, 14401, 14402, 14403, 14405, 14407, 14408, 14409, 14410, 14411, 14413, 14414, 14415, 14417, 14418, 14419, 14421, 14422, 14423, 14425, 14427, 14429, 14431, 14433, 14434, 14435, 14437, 14438, 14439, 14440, 14441, 14443, 14444, 14445, 14446, 14447, 14448, 14449, 14450, 14451, 14452, 14453, 14455, 14456, 14457, 14458, 14459, 14461, 14462, 14463, 14464, 14465, 14467, 14468, 14469, 14470, 14471, 14473, 14475, 14477, 14479, 14480, 14481, 14482, 14483, 14485, 14486, 14487, 14489, 14490, 14491, 14493, 14494, 14495, 14496, 14497, 14498, 14501, 14503, 14505, 14507, 14509, 14511, 14513, 14515, 14516, 14517, 14518, 14519, 14521, 14522, 14523, 14524, 14525, 14527, 14529, 14530, 14531, 14533, 14534, 14535, 14537, 14539, 14540, 14541, 14543, 14545, 14546, 14547, 14548, 14549, 14551, 14553, 14554, 14555, 14557, 14558, 14559, 14560, 14561, 14563, 14564, 14565, 14566, 14567, 14569, 14570, 14571, 14572, 14573, 14575, 14576, 14577, 14578, 14579, 14581, 14582, 14583, 14584, 14585, 14587, 14589, 14590, 14591, 14593, 14594, 14596, 14597, 14599, 14600, 14601, 14602, 14603, 14605, 14606, 14607, 14609, 14611, 14612, 14613, 14614, 14615, 14617, 14618, 14619, 14621, 14623, 14625, 14626, 14627, 14628, 14629, 14630, 14631, 14633, 14635, 14636, 14637, 14638, 14639, 14642, 14643, 14645, 14647, 14649, 14651, 14653, 14654, 14655, 14656, 14657, 14659, 14661, 14662, 14663, 14665, 14666, 14667, 14669, 14671, 14672, 14673, 14674, 14675, 14677, 14679, 14681, 14683, 14685, 14687, 14689, 14690, 14691, 14693, 14695, 14697, 14699, 14701, 14702, 14703, 14705, 14707, 14708, 14709, 14710, 14711, 14713, 14714, 14715, 14717, 14719, 14721, 14722, 14723, 14724, 14725, 14726, 14727, 14728, 14729, 14731, 14732, 14733, 14734, 14735, 14736, 14737, 14739, 14740, 14741, 14743, 14744, 14745, 14746, 14747, 14748, 14749, 14750, 14751, 14753, 14755, 14757, 14758, 14759, 14761, 14762, 14763, 14765, 14767, 14768, 14769, 14770, 14771, 14772, 14773, 14774, 14775, 14776, 14777, 14778, 14779, 14781, 14782, 14783, 14785, 14787, 14788, 14789, 14791, 14792, 14793, 14794, 14795, 14797, 14798, 14799, 14800, 14801, 14803, 14805, 14806, 14807, 14809, 14810, 14811, 14813, 14815, 14817, 14818, 14819, 14821, 14822, 14823, 14824, 14825, 14827, 14828, 14829, 14830, 14831, 14832, 14833, 14835, 14836, 14837, 14839, 14841, 14842, 14843, 14845, 14846, 14847, 14848, 14849, 14851, 14853, 14854, 14855, 14857, 14858, 14859, 14860, 14861, 14863, 14865, 14867, 14868, 14869, 14870, 14871, 14872, 14873, 14875, 14876, 14877, 14878, 14879, 14881, 14882, 14883, 14884, 14885, 14887, 14889, 14890, 14891, 14893, 14894, 14895, 14897, 14899, 14901, 14902, 14903, 14905, 14906, 14907, 14908, 14909, 14911, 14912, 14913, 14914, 14915, 14916, 14917, 14918, 14919, 14921, 14923, 14925, 14926, 14927, 14929, 14930, 14931, 14933, 14935, 14936, 14937, 14939, 14940, 14941, 14942, 14943, 14944, 14945, 14947, 14949, 14950, 14951, 14952, 14953, 14954, 14955, 14957, 14958, 14959, 14961, 14962, 14963, 14964, 14965, 14966, 14967, 14969, 14971, 14972, 14973, 14975, 14977, 14978, 14979, 14980, 14981, 14983, 14984, 14985, 14987, 14989, 14990, 14991, 14992, 14993, 14995, 14996, 14997, 14998, 14999, 15001, 15003, 15004, 15005, 15007, 15009, 15010, 15011, 15013, 15014, 15015, 15017, 15018, 15019, 15021, 15022, 15023, 15025, 15026, 15027, 15029, 15030, 15031, 15033, 15035, 15037, 15038, 15041, 15043, 15044, 15045, 15046, 15047, 15048, 15049, 15050, 15051, 15052, 15053, 15055, 15057, 15059, 15060, 15061, 15063, 15064, 15065, 15067, 15069, 15071, 15073, 15075, 15076, 15077, 15079, 15081, 15082, 15083, 15085, 15086, 15087, 15089, 15091, 15093, 15094, 15097, 15098, 15099, 15101, 15103, 15104, 15105, 15106, 15107, 15109, 15111, 15112, 15113, 15115, 15116, 15117, 15118, 15121, 15122, 15123, 15124, 15125, 15126, 15127, 15129, 15130, 15131, 15132, 15133, 15134, 15135, 15136, 15137, 15138, 15139, 15141, 15143, 15144, 15145, 15146, 15147, 15149, 15151, 15153, 15154, 15155, 15157, 15158, 15159, 15161, 15163, 15164, 15165, 15167, 15168, 15169, 15170, 15171, 15172, 15173, 15175, 15176, 15177, 15178, 15179, 15181, 15182, 15183, 15184, 15185, 15187, 15189, 15191, 15193, 15194, 15195, 15197, 15199, 15201, 15202, 15205, 15206, 15207, 15208, 15209, 15211, 15212, 15213, 15214, 15215, 15217, 15218, 15219, 15220, 15221, 15223, 15225, 15226, 15227, 15229, 15230, 15231, 15233, 15235, 15236, 15237, 15238, 15239, 15241, 15242, 15243, 15245, 15247, 15248, 15249, 15250, 15251, 15253, 15254, 15255, 15256, 15257, 15259, 15261, 15262, 15263, 15265, 15267, 15269, 15271, 15273, 15274, 15275, 15276, 15277, 15278, 15279, 15280, 15281, 15283, 15284, 15285, 15286, 15287, 15289, 15290, 15291, 15292, 15293, 15295, 15296, 15297, 15298, 15299, 15301, 15303, 15304, 15305, 15307, 15308, 15309, 15310, 15311, 15313, 15314, 15315, 15317, 15319, 15321, 15322, 15323, 15325, 15326, 15327, 15328, 15329, 15331, 15332, 15333, 15334, 15335, 15337, 15338, 15339, 15341, 15343, 15345, 15347, 15348, 15349, 15350, 15351, 15352, 15353, 15355, 15356, 15357, 15358, 15359, 15361, 15363, 15365, 15367, 15369, 15370, 15371, 15373, 15375, 15377, 15379, 15381, 15383, 15385, 15386, 15387, 15388, 15389, 15391, 15393, 15394, 15395, 15397, 15398, 15399, 15401, 15403, 15404, 15405, 15406, 15409, 15411, 15412, 15413, 15414, 15415, 15416, 15417, 15418, 15419, 15421, 15422, 15423, 15424, 15425, 15427, 15429, 15430, 15431, 15433, 15434, 15435, 15436, 15437, 15439, 15441, 15442, 15443, 15445, 15446, 15447, 15448, 15449, 15451, 15452, 15453, 15454, 15455, 15457, 15458, 15459, 15461, 15463, 15464, 15465, 15466, 15467, 15469, 15470, 15471, 15473, 15475, 15477, 15478, 15479, 15481, 15482, 15483, 15485, 15487, 15488, 15489, 15491, 15493, 15494, 15495, 15496, 15497, 15499, 15500, 15501, 15502, 15503, 15505, 15507, 15508, 15509, 15511, 15513, 15514, 15515, 15516, 15517, 15518, 15519, 15520, 15521, 15523, 15524, 15525, 15527, 15528, 15529, 15530, 15531, 15532, 15533, 15535, 15536, 15537, 15538, 15539, 15541, 15542, 15543, 15545, 15547, 15549, 15550, 15551, 15553, 15554, 15555, 15556, 15557, 15559, 15561, 15562, 15563, 15565, 15566, 15567, 15568, 15569, 15571, 15572, 15573, 15574, 15575, 15577, 15578, 15579, 15580, 15581, 15583, 15585, 15587, 15589, 15591, 15593, 15595, 15597, 15599, 15601, 15602, 15603, 15604, 15605, 15607, 15608, 15609, 15610, 15611, 15612, 15613, 15614, 15615, 15616, 15617, 15619, 15621, 15623, 15626, 15627, 15629, 15631, 15633, 15635, 15636, 15637, 15638, 15639, 15641, 15643, 15645, 15647, 15649, 15650, 15651, 15653, 15655, 15657, 15658, 15659, 15661, 15662, 15663, 15664, 15665, 15667, 15668, 15669, 15671, 15673, 15675, 15677, 15679, 15681, 15683, 15685, 15686, 15687, 15689, 15690, 15691, 15692, 15693, 15694, 15695, 15697, 15698, 15699, 15701, 15703, 15704, 15705, 15707, 15709, 15710, 15711, 15712, 15713, 15715, 15717, 15718, 15721, 15722, 15723, 15725, 15727, 15728, 15729, 15730, 15731, 15733, 15734, 15735, 15736, 15737, 15739, 15741, 15742, 15743, 15745, 15746, 15747, 15749, 15751, 15752, 15753, 15755, 15756, 15757, 15758, 15759, 15761, 15763, 15765, 15766, 15767, 15769, 15770, 15771, 15772, 15773, 15775, 15776, 15778, 15779, 15780, 15781, 15782, 15783, 15784, 15785, 15787, 15789, 15791, 15793, 15794, 15795, 15796, 15797, 15799, 15801, 15802, 15803, 15805, 15806, 15807, 15809, 15811, 15812, 15813, 15814, 15815, 15817, 15818, 15819, 15821, 15823, 15824, 15825, 15826, 15827, 15829, 15831, 15833, 15835, 15836, 15837, 15839, 15841, 15842, 15843, 15845, 15847, 15848, 15849, 15850, 15851, 15853, 15855, 15857, 15859, 15860, 15861, 15862, 15863, 15865, 15867, 15869, 15871, 15873, 15875, 15876, 15877, 15878, 15879, 15881, 15883, 15884, 15885, 15887, 15888, 15889, 15890, 15891, 15893, 15895, 15896, 15897, 15898, 15899, 15901, 15902, 15903, 15904, 15905, 15907, 15908, 15909, 15910, 15911, 15913, 15914, 15915, 15916, 15917, 15919, 15920, 15921, 15922, 15923, 15925, 15926, 15927, 15929, 15931, 15933, 15934, 15935, 15937, 15938, 15939, 15941, 15943, 15945, 15947, 15949, 15951, 15953, 15955, 15956, 15957, 15958, 15959, 15961, 15962, 15963, 15965, 15967, 15968, 15969, 15970, 15971, 15973, 15974, 15975, 15976, 15977, 15980, 15981, 15982, 15983, 15985, 15986, 15987, 15989, 15991, 15993, 15994, 15995, 15997, 15999, 16001, 16003, 16004, 16005, 16006, 16007, 16009, 16011, 16012, 16013, 16015, 16017, 16018, 16019, 16021, 16022, 16023, 16024, 16025, 16027, 16029, 16030, 16031, 16033, 16035, 16036, 16037, 16040, 16041, 16042, 16043, 16045, 16046, 16047, 16049, 16051, 16052, 16053, 16054, 16055, 16057, 16058, 16059, 16060, 16061, 16063, 16065, 16066, 16067, 16069, 16070, 16071, 16072, 16073, 16075, 16076, 16077, 16078, 16079, 16081, 16082, 16083, 16084, 16085, 16087, 16088, 16089, 16090, 16091, 16092, 16093, 16094, 16095, 16097, 16098, 16099, 16101, 16102, 16103, 16105, 16107, 16109, 16110, 16111, 16113, 16114, 16115, 16117, 16119, 16120, 16121, 16123, 16124, 16125, 16126, 16127, 16129, 16130, 16131, 16133, 16135, 16137, 16138, 16139, 16141, 16142, 16143, 16145, 16147, 16149, 16150, 16151, 16153, 16154, 16155, 16157, 16159, 16161, 16163, 16164, 16165, 16166, 16167, 16169, 16171, 16173, 16174, 16175, 16176, 16177, 16179, 16180, 16181, 16183, 16185, 16187, 16188, 16189, 16190, 16191, 16192, 16193, 16195, 16196, 16197, 16199, 16200, 16201, 16203, 16205, 16207, 16208, 16209, 16210, 16211, 16213, 16214, 16215, 16216, 16217, 16219, 16221, 16223, 16225, 16227, 16228, 16229, 16231, 16232, 16233, 16235, 16237, 16238, 16239, 16240, 16241, 16243, 16244, 16245, 16246, 16247, 16249, 16250, 16251, 16253, 16255, 16257, 16259, 16260, 16261, 16262, 16263, 16265, 16267, 16269, 16270, 16271, 16273, 16275, 16276, 16277, 16279, 16281, 16282, 16283, 16285, 16286, 16287, 16288, 16289, 16291, 16293, 16294, 16295, 16297, 16298, 16299, 16301, 16303, 16305, 16307, 16308, 16309, 16310, 16311, 16313, 16315, 16316, 16317, 16318, 16319, 16321, 16323, 16325, 16327, 16328, 16329, 16330, 16331, 16333, 16335, 16337, 16339, 16340, 16341, 16342, 16343, 16345, 16346, 16347, 16349, 16351, 16352, 16353, 16354, 16356, 16357, 16358, 16359, 16360, 16361, 16363, 16365, 16366, 16367, 16369, 16370, 16371, 16372, 16373, 16375, 16376, 16377, 16379, 16381, 16382, 16385, 16387, 16388, 16389, 16391, 16393, 16395, 16397, 16399, 16400, 16401, 16402, 16403, 16405, 16406, 16407, 16408, 16409, 16411, 16412, 16413, 16414, 16415, 16417, 16418, 16419, 16420, 16421, 16423, 16424, 16425, 16426, 16427, 16429, 16430, 16431, 16432, 16433, 16435, 16437, 16438, 16439, 16441, 16442, 16443, 16444, 16445, 16447, 16448, 16449, 16450, 16451, 16453, 16454, 16455, 16456, 16457, 16459, 16461, 16462, 16463, 16464, 16465, 16466, 16467, 16468, 16469, 16471, 16473, 16475, 16476, 16477, 16478, 16479, 16480, 16481, 16483, 16485, 16486, 16487, 16489, 16490, 16491, 16493, 16495, 16496, 16497, 16498, 16499, 16501, 16503, 16504, 16505, 16507, 16509, 16510, 16511, 16513, 16514, 16515, 16517, 16519, 16521, 16522, 16523, 16525, 16526, 16527, 16529, 16531, 16532, 16533, 16535, 16537, 16538, 16539, 16541, 16543, 16545, 16546, 16547, 16549, 16550, 16551, 16552, 16553, 16555, 16556, 16557, 16558, 16559, 16560, 16561, 16562, 16563, 16565, 16566, 16567, 16568, 16569, 16570, 16571, 16572, 16573, 16574, 16575, 16577, 16579, 16580, 16581, 16582, 16583, 16585, 16586, 16587, 16588, 16589, 16591, 16593, 16595, 16597, 16598, 16599, 16600, 16601, 16603, 16605, 16606, 16607, 16609, 16611, 16612, 16613, 16615, 16616, 16617, 16618, 16619, 16621, 16622, 16623, 16624, 16625, 16627, 16628, 16629, 16630, 16631, 16633, 16635, 16637, 16639, 16642, 16643, 16645, 16646, 16647, 16648, 16649, 16651, 16652, 16653, 16654, 16657, 16658, 16659, 16661, 16663, 16664, 16665, 16666, 16667, 16668, 16669, 16670, 16671, 16672, 16673, 16675, 16677, 16678, 16679, 16681, 16682, 16683, 16685, 16687, 16688, 16689, 16690, 16691, 16692, 16693, 16695, 16697, 16699, 16700, 16701, 16702, 16703, 16705, 16706, 16707, 16708, 16709, 16711, 16712, 16713, 16714, 16715, 16717, 16718, 16719, 16720, 16721, 16722, 16723, 16725, 16726, 16727, 16729, 16730, 16731, 16732, 16733, 16735, 16736, 16737, 16739, 16740, 16741, 16743, 16745, 16747, 16748, 16749, 16751, 16753, 16754, 16755, 16757, 16759, 16760, 16761, 16763, 16764, 16765, 16766, 16767, 16769, 16771, 16773, 16774, 16775, 16777, 16778, 16779, 16780, 16781, 16783, 16784, 16785, 16786, 16787, 16788, 16789, 16790, 16791, 16792, 16793, 16795, 16796, 16797, 16798, 16799, 16801, 16802, 16803, 16804, 16805, 16807, 16808, 16809, 16810, 16811, 16815, 16816, 16817, 16819, 16820, 16821, 16822, 16823, 16825, 16826, 16827, 16829, 16831, 16833, 16834, 16835, 16837, 16838, 16839, 16841, 16843, 16845, 16846, 16847, 16848, 16850, 16851, 16852, 16853, 16855, 16856, 16857, 16859, 16861, 16862, 16863, 16865, 16867, 16869, 16870, 16871, 16873, 16874, 16875, 16877, 16878, 16879, 16880, 16881, 16883, 16885, 16886, 16887, 16888, 16889, 16891, 16893, 16894, 16895, 16897, 16899, 16900, 16901, 16903, 16904, 16905, 16906, 16907, 16909, 16911, 16912, 16913, 16915, 16917, 16918, 16919, 16921, 16922, 16923, 16924, 16925, 16927, 16928, 16929, 16931, 16932, 16933, 16935, 16937, 16939, 16941, 16942, 16943, 16944, 16945, 16947, 16949, 16951, 16952, 16953, 16954, 16955, 16956, 16957, 16958, 16959, 16961, 16963, 16964, 16965, 16966, 16967, 16968, 16969, 16970, 16971, 16973, 16975, 16977, 16979, 16981, 16982, 16983, 16985, 16987, 16988, 16989, 16991, 16992, 16993, 16995, 16997, 16999, 17000, 17001, 17002, 17003, 17004, 17005, 17006, 17007, 17008, 17009, 17011, 17012, 17013, 17014, 17015, 17017, 17018, 17019, 17020, 17021, 17023, 17025, 17027, 17029, 17031, 17033, 17035, 17036, 17037, 17038, 17039, 17041, 17042, 17043, 17044, 17045, 17046, 17047, 17049, 17050, 17051, 17053, 17054, 17055, 17057, 17059, 17061, 17062, 17063, 17064, 17065, 17066, 17067, 17069, 17071, 17073, 17075, 17076, 17077, 17078, 17079, 17081, 17083, 17084, 17085, 17086, 17087, 17089, 17090, 17091, 17093, 17094, 17095, 17097, 17099, 17101, 17102, 17103, 17104, 17105, 17107, 17109, 17110, 17111, 17113, 17114, 17115, 17117, 17119, 17120, 17121, 17122, 17123, 17125, 17126, 17127, 17129, 17131, 17133, 17134, 17135, 17137, 17138, 17139, 17140, 17141, 17145, 17147, 17149, 17150, 17151, 17153, 17155, 17156, 17157, 17158, 17159, 17161, 17163, 17164, 17165, 17167, 17169, 17170, 17171, 17173, 17174, 17175, 17177, 17179, 17180, 17181, 17182, 17183, 17185, 17186, 17188, 17189, 17191, 17192, 17193, 17195, 17197, 17198, 17199, 17200, 17201, 17203, 17205, 17207, 17209, 17211, 17213, 17215, 17217, 17218, 17219, 17220, 17221, 17222, 17223, 17224, 17225, 17227, 17228, 17229, 17230, 17231, 17233, 17234, 17235, 17237, 17239, 17241, 17242, 17244, 17245, 17246, 17247, 17249, 17251, 17253, 17254, 17255, 17257, 17259, 17261, 17263, 17264, 17265, 17266, 17267, 17268, 17269, 17271, 17273, 17275, 17279, 17280, 17281, 17282, 17283, 17284, 17285, 17287, 17289, 17291, 17293, 17295, 17297, 17298, 17299, 17300, 17301, 17302, 17303, 17305, 17306, 17307, 17309, 17310, 17311, 17312, 17313, 17314, 17315, 17317, 17319, 17321, 17323, 17324, 17325, 17326, 17327, 17329, 17330, 17331, 17333, 17335, 17336, 17337, 17338, 17339, 17340, 17341, 17342, 17343, 17344, 17345, 17347, 17348, 17349, 17350, 17351, 17353, 17355, 17356, 17357, 17359, 17361, 17363, 17364, 17365, 17366, 17367, 17369, 17370, 17371, 17372, 17373, 17374, 17375, 17377, 17379, 17380, 17381, 17383, 17385, 17386, 17387, 17389, 17390, 17391, 17393, 17395, 17396, 17397, 17398, 17399, 17401, 17402, 17403, 17405, 17407, 17408, 17409, 17410, 17411, 17412, 17414, 17415, 17416, 17417, 17419, 17421, 17422, 17423, 17424, 17425, 17426, 17427, 17428, 17429, 17431, 17433, 17434, 17435, 17436, 17437, 17438, 17439, 17440, 17441, 17443, 17444, 17445, 17446, 17447, 17449, 17451, 17453, 17455, 17457, 17458, 17459, 17461, 17462, 17463, 17464, 17465, 17467, 17469, 17470, 17471, 17473, 17474, 17475, 17477, 17479, 17480, 17481, 17483, 17484, 17485, 17486, 17487, 17488, 17489, 17491, 17492, 17493, 17494, 17495, 17497, 17498, 17499, 17501, 17503, 17504, 17505, 17506, 17507, 17508, 17509, 17511, 17512, 17513, 17515, 17517, 17519, 17520, 17521, 17523, 17525, 17527, 17529, 17531, 17532, 17533, 17534, 17535, 17536, 17537, 17539, 17541, 17542, 17543, 17545, 17546, 17547, 17548, 17549, 17551, 17552, 17554, 17555, 17557, 17558, 17559, 17561, 17563, 17564, 17565, 17566, 17567, 17569, 17571, 17573, 17575, 17577, 17579, 17581, 17582, 17583, 17585, 17587, 17588, 17589, 17590, 17591, 17593, 17594, 17595, 17597, 17599, 17601, 17602, 17603, 17605, 17606, 17607, 17608, 17609, 17611, 17613, 17614, 17615, 17617, 17618, 17619, 17621, 17623, 17624, 17625, 17626, 17627, 17629, 17631, 17632, 17633, 17635, 17636, 17637, 17638, 17639, 17641, 17643, 17644, 17645, 17647, 17649, 17651, 17652, 17653, 17654, 17655, 17656, 17657, 17659, 17661, 17662, 17663, 17665, 17669, 17671, 17672, 17673, 17675, 17677, 17678, 17679, 17680, 17681, 17683, 17684, 17685, 17686, 17687, 17689, 17691, 17692, 17693, 17695, 17696, 17697, 17698, 17699, 17701, 17702, 17703, 17705, 17707, 17708, 17709, 17710, 17711, 17713, 17714, 17715, 17717, 17719, 17721, 17723, 17725, 17726, 17727, 17729, 17731, 17732, 17733, 17734, 17735, 17737, 17738, 17739, 17740, 17741, 17743, 17744, 17745, 17746, 17747, 17749, 17751, 17752, 17753, 17755, 17756, 17757, 17758, 17759, 17761, 17762, 17763, 17764, 17765, 17767, 17768, 17769, 17770, 17771, 17773, 17775, 17776, 17777, 17779, 17781, 17783, 17785, 17786, 17787, 17788, 17789, 17791, 17792, 17793, 17794, 17795, 17796, 17797, 17798, 17799, 17800, 17801, 17803, 17805, 17806, 17807, 17809, 17810, 17811, 17813, 17815, 17816, 17817, 17819, 17821, 17822, 17823, 17824, 17825, 17827, 17829, 17830, 17833, 17834, 17835, 17836, 17837, 17839, 17840, 17841, 17842, 17843, 17845, 17846, 17847, 17849, 17851, 17852, 17853, 17854, 17855, 17856, 17857, 17859, 17860, 17861, 17863, 17864, 17865, 17866, 17867, 17868, 17869, 17870, 17871, 17872, 17873, 17875, 17876, 17877, 17878, 17879, 17881, 17883, 17885, 17887, 17889, 17890, 17891, 17893, 17894, 17895, 17897, 17899, 17900, 17901, 17902, 17903, 17905, 17907, 17908, 17909, 17911, 17913, 17915, 17916, 17917, 17918, 17919, 17920, 17921, 17923, 17924, 17925, 17926, 17927, 17928, 17929, 17930, 17931, 17932, 17933, 17935, 17937, 17938, 17939, 17941, 17942, 17943, 17945, 17947, 17949, 17950, 17951, 17953, 17954, 17955, 17956, 17957, 17959, 17961, 17962, 17963, 17965, 17966, 17967, 17969, 17971, 17972, 17973, 17974, 17975, 17977, 17978, 17979, 17981, 17983, 17984, 17985, 17987, 17989, 17991, 17992, 17993, 17995, 17996, 17997, 17998, 17999, 18001, 18003, 18005, 18007, 18008, 18009, 18011, 18013, 18014, 18015, 18017, 18019, 18020, 18021, 18022, 18023, 18025, 18026, 18027, 18028, 18029, 18031, 18033, 18035, 18037, 18039, 18041, 18043, 18044, 18045, 18046, 18047, 18049, 18050, 18051, 18052, 18053, 18054, 18055, 18056, 18057, 18058, 18059, 18061, 18062, 18063, 18064, 18065, 18067, 18068, 18069, 18071, 18073, 18074, 18075, 18076, 18077, 18079, 18080, 18081, 18083, 18085, 18086, 18087, 18088, 18089, 18091, 18092, 18093, 18094, 18095, 18097, 18099, 18100, 18101, 18103, 18104, 18105, 18106, 18107, 18109, 18111, 18112, 18113, 18115, 18117, 18118, 18119, 18121, 18122, 18123, 18125, 18127, 18128, 18129, 18130, 18131, 18133, 18135, 18136, 18137, 18139, 18140, 18141, 18142, 18143, 18145, 18146, 18147, 18149, 18151, 18152, 18153, 18154, 18155, 18157, 18159, 18161, 18163, 18164, 18165, 18166, 18167, 18168, 18169, 18171, 18173, 18175, 18177, 18178, 18179, 18181, 18182, 18183, 18184, 18185, 18187, 18189, 18190, 18191, 18192, 18193, 18194, 18195, 18196, 18197, 18199, 18201, 18202, 18203, 18205, 18206, 18207, 18208, 18209, 18211, 18213, 18214, 18215, 18217, 18218, 18219, 18221, 18223, 18225, 18226, 18227, 18229, 18230, 18231, 18232, 18233, 18235, 18237, 18238, 18239, 18241, 18242, 18243, 18244, 18245, 18247, 18249, 18250, 18251, 18252, 18253, 18254, 18255, 18257, 18259, 18261, 18262, 18263, 18265, 18267, 18269, 18270, 18271, 18272, 18273, 18275, 18277, 18278, 18279, 18280, 18281, 18283, 18285, 18286, 18287, 18288, 18289, 18290, 18291, 18292, 18293, 18295, 18296, 18297, 18298, 18299, 18300, 18301, 18302, 18303, 18304, 18305, 18307, 18308, 18309, 18310, 18311, 18313, 18315, 18317, 18319, 18321, 18322, 18323, 18325, 18326, 18327, 18328, 18329, 18331, 18333, 18334, 18335, 18337, 18338, 18339, 18341, 18343, 18344, 18345, 18347, 18348, 18349, 18351, 18353, 18355, 18357, 18358, 18359, 18361, 18362, 18363, 18364, 18365, 18367, 18368, 18369, 18370, 18371, 18373, 18374, 18375, 18376, 18377, 18379, 18380, 18381, 18382, 18383, 18385, 18386, 18387, 18389, 18391, 18392, 18393, 18394, 18395, 18397, 18398, 18399, 18401, 18402, 18403, 18404, 18405, 18406, 18407, 18408, 18409, 18410, 18411, 18413, 18414, 18415, 18417, 18419, 18421, 18422, 18423, 18424, 18425, 18427, 18429, 18430, 18431, 18432, 18433, 18434, 18435, 18437, 18439, 18441, 18442, 18443, 18445, 18446, 18447, 18448, 18449, 18451, 18453, 18455, 18457, 18458, 18459, 18460, 18461, 18463, 18464, 18465, 18466, 18467, 18469, 18470, 18471, 18473, 18475, 18476, 18477, 18478, 18479, 18481, 18483, 18484, 18485, 18487, 18488, 18489, 18491, 18493, 18494, 18495, 18496, 18497, 18499, 18500, 18501, 18502, 18503, 18505, 18506, 18507, 18509, 18511, 18512, 18513, 18514, 18515, 18517, 18518, 18519, 18521, 18523, 18524, 18525, 18526, 18527, 18529, 18530, 18531, 18532, 18533, 18535, 18536, 18537, 18539, 18541, 18543, 18545, 18547, 18548, 18549, 18553, 18555, 18556, 18557, 18559, 18560, 18561, 18562, 18563, 18565, 18566, 18567, 18569, 18571, 18573, 18575, 18576, 18578, 18579, 18580, 18581, 18583, 18584, 18585, 18587, 18589, 18591, 18593, 18595, 18596, 18597, 18598, 18599, 18601, 18602, 18603, 18605, 18607, 18609, 18610, 18611, 18613, 18614, 18615, 18617, 18619, 18621, 18622, 18623, 18626, 18627, 18628, 18629, 18631, 18632, 18633, 18635, 18636, 18637, 18639, 18640, 18641, 18643, 18645, 18646, 18647, 18649, 18651, 18652, 18653, 18655, 18656, 18657, 18658, 18661, 18662, 18663, 18664, 18665, 18667, 18668, 18669, 18670, 18671, 18673, 18674, 18675, 18677, 18679, 18681, 18683, 18685, 18686, 18687, 18689, 18691, 18692, 18693, 18694, 18695, 18697, 18699, 18700, 18701, 18703, 18705, 18707, 18709, 18711, 18712, 18713, 18715, 18716, 18717, 18719, 18721, 18722, 18723, 18725, 18727, 18728, 18729, 18731, 18733, 18734, 18735, 18737, 18739, 18741, 18742, 18743, 18744, 18745, 18747, 18748, 18749, 18751, 18753, 18755, 18757, 18758, 18759, 18761, 18763, 18764, 18765, 18766, 18767, 18771, 18772, 18773, 18774, 18775, 18776, 18777, 18779, 18781, 18782, 18783, 18785, 18787, 18789, 18790, 18791, 18793, 18795, 18797, 18799, 18801, 18802, 18803, 18804, 18805, 18806, 18807, 18809, 18811, 18812, 18813, 18815, 18817, 18818, 18819, 18820, 18821, 18823, 18825, 18827, 18828, 18829, 18830, 18831, 18833, 18835, 18836, 18837, 18838, 18839, 18841, 18843, 18845, 18847, 18849, 18850, 18851, 18852, 18853, 18855, 18856, 18857, 18859, 18860, 18861, 18862, 18863, 18865, 18867, 18869, 18871, 18872, 18873, 18875, 18877, 18878, 18879, 18881, 18882, 18883, 18884, 18885, 18887, 18889, 18890, 18891, 18892, 18893, 18895, 18896, 18897, 18898, 18899, 18901, 18902, 18903, 18904, 18905, 18907, 18908, 18909, 18910, 18911, 18913, 18914, 18915, 18917, 18919, 18921, 18923, 18925, 18927, 18928, 18929, 18931, 18933, 18934, 18935, 18937, 18938, 18939, 18940, 18941, 18943, 18944, 18945, 18947, 18948, 18949, 18951, 18952, 18953, 18954, 18955, 18956, 18957, 18958, 18959, 18961, 18962, 18963, 18964, 18965, 18967, 18968, 18969, 18970, 18971, 18973, 18974, 18975, 18976, 18977, 18979, 18980, 18981, 18982, 18983, 18985, 18986, 18987, 18988, 18989, 18991, 18992, 18993, 18994, 18995, 18996, 18997, 18998, 18999, 19000, 19001, 19003, 19004, 19005, 19006, 19007, 19009, 19010, 19011, 19012, 19013, 19015, 19016, 19017, 19018, 19019, 19020, 19021, 19022, 19023, 19025, 19027, 19029, 19031, 19033, 19034, 19035, 19036, 19037, 19039, 19041, 19042, 19043, 19044, 19045, 19046, 19047, 19048, 19049, 19051, 19053, 19054, 19055, 19057, 19058, 19059, 19060, 19061, 19063, 19065, 19066, 19067, 19069, 19070, 19071, 19072, 19073, 19075, 19077, 19079, 19080, 19081, 19082, 19083, 19085, 19087, 19088, 19089, 19090, 19091, 19092, 19093, 19095, 19097, 19099, 19101, 19103, 19104, 19105, 19106, 19107, 19108, 19109, 19111, 19113, 19114, 19115, 19117, 19118, 19119, 19121, 19123, 19125, 19127, 19129, 19131, 19132, 19135, 19136, 19137, 19138, 19139, 19141, 19142, 19143, 19144, 19145, 19147, 19148, 19149, 19150, 19151, 19152, 19153, 19154, 19155, 19156, 19157, 19159, 19161, 19163, 19165, 19166, 19167, 19168, 19169, 19171, 19172, 19173, 19174, 19175, 19177, 19178, 19179, 19181, 19183, 19185, 19186, 19187, 19189, 19191, 19192, 19193, 19194, 19195, 19197, 19199, 19201, 19202, 19203, 19204, 19205, 19207, 19208, 19209, 19210, 19211, 19212, 19213, 19214, 19215, 19216, 19217, 19219, 19220, 19221, 19222, 19223, 19225, 19226, 19227, 19228, 19229, 19231, 19232, 19233, 19235, 19237, 19238, 19239, 19241, 19243, 19245, 19246, 19247, 19249, 19250, 19251, 19252, 19253, 19255, 19257, 19258, 19259, 19261, 19262, 19263, 19265, 19267, 19268, 19269, 19270, 19271, 19273, 19274, 19275, 19277, 19279, 19281, 19282, 19283, 19285, 19286, 19287, 19289, 19291, 19293, 19295, 19296, 19297, 19298, 19299, 19301, 19303, 19305, 19307, 19308, 19309, 19310, 19311, 19313, 19315, 19317, 19318, 19319, 19321, 19322, 19323, 19325, 19327, 19328, 19329, 19330, 19331, 19333, 19334, 19335, 19337, 19339, 19340, 19341, 19342, 19343, 19345, 19347, 19349, 19351, 19352, 19353, 19355, 19357, 19358, 19359, 19360, 19361, 19363, 19364, 19365, 19366, 19367, 19368, 19369, 19370, 19371, 19372, 19373, 19375, 19377, 19379, 19381, 19382, 19383, 19385, 19387, 19389, 19391, 19393, 19395, 19397, 19399, 19401, 19402, 19403, 19405, 19406, 19407, 19408, 19409, 19411, 19413, 19415, 19417, 19418, 19419, 19420, 19421, 19423, 19425, 19426, 19427, 19428, 19429, 19431, 19432, 19433, 19435, 19437, 19438, 19439, 19441, 19442, 19443, 19444, 19445, 19447, 19448, 19449, 19450, 19451, 19453, 19454, 19455, 19456, 19457, 19459, 19461, 19462, 19463, 19465, 19466, 19467, 19469, 19471, 19472, 19473, 19475, 19476, 19477, 19478, 19479, 19481, 19483, 19485, 19486, 19487, 19489, 19490, 19493, 19495, 19497, 19498, 19499, 19501, 19503, 19505, 19507, 19508, 19509, 19510, 19511, 19513, 19514, 19515, 19517, 19519, 19520, 19521, 19522, 19523, 19524, 19525, 19526, 19527, 19528, 19529, 19531, 19532, 19533, 19534, 19535, 19536, 19537, 19539, 19541, 19543, 19544, 19545, 19546, 19547, 19548, 19549, 19550, 19551, 19552, 19553, 19555, 19556, 19557, 19558, 19559, 19561, 19563, 19565, 19567, 19568, 19569, 19570, 19571, 19574, 19575, 19577, 19579, 19580, 19581, 19582, 19583, 19585, 19586, 19587, 19588, 19589, 19591, 19593, 19594, 19595, 19597, 19598, 19600, 19601, 19602, 19603, 19605, 19606, 19607, 19609, 19610, 19611, 19613, 19615, 19616, 19617, 19618, 19619, 19621, 19622, 19623, 19624, 19625, 19627, 19629, 19630, 19631, 19632, 19633, 19634, 19635, 19636, 19637, 19639, 19640, 19641, 19642, 19643, 19645, 19646, 19647, 19649, 19651, 19652, 19653, 19654, 19655, 19657, 19658, 19659, 19661, 19663, 19664, 19665, 19667, 19669, 19671, 19672, 19673, 19675, 19677, 19678, 19679, 19681, 19682, 19683, 19685, 19687, 19688, 19689, 19691, 19692, 19693, 19694, 19695, 19696, 19697, 19699, 19700, 19701, 19702, 19703, 19705, 19706, 19707, 19708, 19709, 19711, 19713, 19714, 19715, 19717, 19718, 19719, 19721, 19722, 19723, 19724, 19725, 19727, 19729, 19730, 19731, 19732, 19733, 19735, 19736, 19737, 19738, 19739, 19741, 19743, 19745, 19747, 19748, 19749, 19751, 19753, 19755, 19756, 19757, 19759, 19761, 19762, 19763, 19764, 19765, 19766, 19767, 19768, 19769, 19771, 19772, 19773, 19774, 19775, 19776, 19777, 19778, 19779, 19781, 19783, 19784, 19785, 19786, 19787, 19789, 19790, 19791, 19793, 19795, 19796, 19797, 19798, 19799, 19801, 19802, 19803, 19804, 19805, 19807, 19808, 19809, 19810, 19811, 19812, 19813, 19814, 19815, 19817, 19819, 19821, 19822, 19823, 19825, 19826, 19827, 19828, 19829, 19831, 19832, 19833, 19834, 19835, 19837, 19838, 19839, 19840, 19841, 19843, 19844, 19845, 19846, 19847, 19849, 19850, 19851, 19853, 19855, 19856, 19857, 19858, 19859, 19861, 19862, 19863, 19865, 19867, 19868, 19869, 19870, 19871, 19873, 19874, 19875, 19876, 19877, 19879, 19881, 19882, 19883, 19884, 19885, 19886, 19887, 19889, 19891, 19892, 19893, 19895, 19897, 19898, 19899, 19900, 19901, 19903, 19905, 19906, 19907, 19909, 19910, 19911, 19912, 19913, 19914, 19915, 19917, 19918, 19919, 19920, 19921, 19923, 19924, 19925, 19926, 19927, 19928, 19929, 19930, 19931, 19934, 19935, 19937, 19939, 19941, 19942, 19943, 19945, 19946, 19947, 19949, 19951, 19953, 19954, 19955, 19956, 19957, 19959, 19961, 19962, 19963, 19965, 19966, 19967, 19969, 19970, 19971, 19973, 19975, 19976, 19978, 19979, 19980, 19981, 19982, 19983, 19984, 19985, 19987, 19989, 19991, 19993, 19994, 19995, 19996, 19997, 19999, 20000] \n\nNumbers that exceeded m: [840, 1074, 1086, 1098, 1248, 1316, 1320, 1372, 1428, 1464, 1512, 1560, 1794, 1848, 1876, 1932, 1992, 2040, 2136, 2238, 2250, 2256, 2280, 2340, 2424, 2430, 2448, 2484, 2568, 2604, 2712, 2716, 2718, 2760, 2772, 2864, 2880, 2940, 3000, 3025, 3048, 3050, 3156, 3210, 3264, 3288, 3312, 3444, 3456, 3472, 3480, 3486, 3492, 3556, 3564, 3612, 3630, 3678, 3690, 3696, 3720, 3746, 3790, 3796, 3834, 3836, 3892, 3912, 3948, 4016, 4086, 4122, 4128, 4170, 4230, 4236, 4296, 4392, 4422, 4440, 4464, 4488, 4500, 4564, 4566, 4578, 4620, 4632, 4648, 4788, 4800, 4806, 4830, 4842, 4848, 4920, 4992, 5088, 5094, 5148, 5250, 5292, 5304, 5370, 5394, 5400, 5426, 5432, 5448, 5456, 5508, 5536, 5640, 5664, 5676, 5688, 5722, 5736, 5796, 5880, 5898, 5908, 5910, 5928, 5946, 5958, 5964, 5982, 5994, 6076, 6078, 6090, 6114, 6126, 6138, 6160, 6174, 6184, 6240, 6244, 6282, 6300, 6306, 6318, 6328, 6342, 6360, 6402, 6448, 6480, 6504, 6534, 6552, 6600, 6636, 6648, 6688, 6690, 6692, 6744, 6748, 6804, 6882, 6960, 6966, 6972, 6978, 6984, 6990, 7002, 7008, 7026, 7032, 7038, 7110, 7230, 7266, 7320, 7352, 7364, 7368, 7412, 7420, 7440, 7458, 7482, 7542, 7586, 7590, 7596, 7614, 7666, 7698, 7710, 7752, 7756, 7770, 7778, 7800, 7812, 7950, 7968, 8015, 8024, 8026, 8034, 8040, 8070, 8080, 8092, 8136, 8148, 8164, 8176, 8190, 8204, 8208, 8232, 8238, 8250, 8260, 8262, 8322, 8328, 8346, 8358, 8388, 8418, 8427, 8432, 8472, 8476, 8496, 8520, 8532, 8632, 8648, 8664, 8802, 8814, 8826, 8838, 8872, 8932, 8958, 8970, 8988, 8994, 9000, 9006, 9008, 9024, 9030, 9048, 9100, 9108, 9120, 9122, 9156, 9168, 9192, 9196, 9240, 9246, 9280, 9288, 9336, 9354, 9366, 9378, 9380, 9390, 9424, 9426, 9436, 9438, 9456, 9480, 9492, 9540, 9588, 9684, 9696, 9708, 9714, 9716, 9726, 9738, 9750, 9772, 9786, 9798, 9810, 9816, 9828, 9840, 9848, 9858, 9912, 9936, 10020, 10032, 10108, 10116, 10140, 10164, 10176, 10182, 10194, 10200, 10206, 10290, 10314, 10326, 10338, 10344, 10350, 10408, 10416, 10464, 10528, 10608, 10612, 10632, 10668, 10724, 10740, 10780, 10842, 10866, 10872, 10876, 10878, 10890, 10892, 10902, 10932, 10938, 10948, 10950, 10962, 10980, 11064, 11088, 11112, 11120, 11144, 11190, 11228, 11232, 11264, 11284, 11298, 11370, 11374, 11394, 11400, 11412, 11452, 11496, 11502, 11508, 11580, 11598, 11610, 11640, 11676, 11692, 11696, 11732, 11742, 11780, 11788, 11790, 11800, 11814, 11826, 11844, 11900, 11908, 12036, 12048, 12095, 12108, 12120, 12126, 12138, 12146, 12240, 12252, 12280, 12294, 12360, 12408, 12450, 12456, 12475, 12516, 12540, 12552, 12582, 12588, 12666, 12678, 12690, 12720, 12726, 12762, 12768, 12796, 12828, 12840, 12850, 12852, 12856, 12906, 12954, 12972, 12974, 13014, 13064, 13080, 13116, 13146, 13170, 13188, 13200, 13216, 13218, 13230, 13244, 13280, 13290, 13300, 13302, 13332, 13378, 13392, 13412, 13468, 13494, 13524, 13536, 13560, 13580, 13592, 13608, 13636, 13656, 13664, 13668, 13692, 13736, 13748, 13800, 13804, 13848, 13860, 13868, 13936, 13972, 14010, 14028, 14034, 14040, 14046, 14056, 14058, 14064, 14082, 14094, 14106, 14118, 14148, 14152, 14160, 14196, 14214, 14232, 14268, 14280, 14322, 14382, 14384, 14388, 14404, 14472, 14492, 14502, 14512, 14514, 14592, 14598, 14604, 14622, 14634, 14640, 14641, 14676, 14682, 14688, 14694, 14698, 14700, 14706, 14756, 14784, 14796, 14802, 14814, 14826, 14834, 14886, 14920, 14922, 14924, 14928, 14970, 15000, 15012, 15036, 15095, 15096, 15100, 15114, 15148, 15160, 15162, 15166, 15174, 15204, 15222, 15240, 15260, 15282, 15288, 15316, 15336, 15360, 15372, 15376, 15380, 15390, 15396, 15407, 15440, 15456, 15462, 15480, 15484, 15498, 15506, 15522, 15546, 15558, 15570, 15576, 15584, 15606, 15624, 15684, 15708, 15720, 15724, 15726, 15738, 15762, 15768, 15774, 15832, 15868, 15882, 15894, 15900, 15930, 15932, 15942, 15954, 15960, 15966, 15978, 15988, 15990, 16008, 16026, 16038, 16044, 16050, 16056, 16068, 16086, 16100, 16144, 16152, 16172, 16178, 16182, 16184, 16220, 16242, 16254, 16268, 16278, 16290, 16302, 16304, 16314, 16322, 16324, 16326, 16364, 16368, 16380, 16416, 16436, 16440, 16446, 16458, 16460, 16470, 16482, 16492, 16542, 16554, 16576, 16578, 16584, 16592, 16608, 16620, 16626, 16641, 16656, 16728, 16770, 16812, 16858, 16902, 16908, 16936, 16960, 16998, 17010, 17024, 17058, 17070, 17088, 17100, 17112, 17132, 17176, 17202, 17248, 17256, 17258, 17270, 17304, 17322, 17334, 17360, 17400, 17404, 17406, 17442, 17448, 17450, 17490, 17500, 17516, 17526, 17544, 17556, 17562, 17568, 17574, 17584, 17586, 17634, 17646, 17648, 17668, 17682, 17694, 17706, 17712, 17724, 17760, 17778, 17790, 17814, 17826, 17828, 17838, 17862, 17884, 17892, 17914, 17948, 17958, 17976, 17994, 18004, 18006, 18016, 18018, 18030, 18060, 18066, 18078, 18090, 18096, 18102, 18120, 18144, 18148, 18204, 18228, 18240, 18264, 18336, 18360, 18462, 18472, 18490, 18498, 18510, 18528, 18554, 18572, 18582, 18606, 18654, 18660, 18666, 18676, 18678, 18680, 18702, 18720, 18740, 18754, 18768, 18786, 18788, 18798, 18800, 18810, 18824, 18840, 18842, 18864, 18866, 18888, 18906, 18936, 18960, 19008, 19030, 19040, 19052, 19056, 19086, 19098, 19146, 19158, 19188, 19196, 19200, 19224, 19284, 19292, 19302, 19314, 19320, 19326, 19338, 19348, 19350, 19376, 19380, 19388, 19396, 19398, 19404, 19410, 19440, 19500, 19502, 19538, 19560, 19572, 19584, 19596, 19614, 19620, 19626, 19628, 19638, 19650, 19656, 19662, 19680, 19684, 19686, 19710, 19728, 19740, 19782, 19824, 19848, 19852, 19864, 19888, 19908, 19938, 19944, 19950, 19964, 19968] \n\nNumbers that reached term m, the input: [138, 150, 168, 180, 210, 222, 234, 264, 276, 306, 312, 318, 330, 354, 360, 366, 378, 396, 456, 480, 498, 510, 528, 534, 546, 552, 564, 570, 582, 594, 600, 612, 642, 654, 660, 696, 702, 720, 726, 750, 780, 786, 798, 822, 828, 834, 846, 858, 864, 870, 888, 930, 936, 960, 966, 978, 990, 996, 1026, 1032, 1044, 1062, 1104, 1122, 1134, 1146, 1148, 1158, 1170, 1204, 1218, 1230, 1260, 1266, 1278, 1290, 1302, 1314, 1326, 1338, 1350, 1356, 1362, 1374, 1386, 1392, 1398, 1410, 1422, 1440, 1476, 1482, 1488, 1494, 1506, 1518, 1521, 1530, 1542, 1554, 1572, 1578, 1590, 1596, 1608, 1620, 1632, 1650, 1656, 1662, 1674, 1680, 1686, 1698, 1704, 1710, 1722, 1734, 1758, 1770, 1782, 1806, 1818, 1820, 1836, 1842, 1854, 1860, 1866, 1872, 1878, 1890, 1896, 1902, 1914, 1920, 1938, 1944, 1950, 1962, 1986, 1998, 2010, 2046, 2058, 2082, 2088, 2094, 2106, 2112, 2124, 2142, 2154, 2160, 2166, 2190, 2202, 2208, 2212, 2214, 2226, 2232, 2262, 2268, 2292, 2298, 2310, 2322, 2328, 2334, 2346, 2352, 2356, 2358, 2360, 2370, 2382, 2394, 2402, 2406, 2418, 2436, 2442, 2472, 2478, 2480, 2490, 2502, 2514, 2526, 2538, 2544, 2550, 2562, 2574, 2580, 2616, 2622, 2640, 2658, 2660, 2664, 2670, 2682, 2724, 2742, 2754, 2766, 2778, 2784, 2790, 2802, 2808, 2814, 2820, 2826, 2828, 2838, 2840, 2850, 2856, 2862, 2874, 2884, 2886, 2898, 2904, 2910, 2912, 2922, 2934, 2946, 2952, 2958, 2960, 2970, 2976, 2982, 2996, 3012, 3018, 3024, 3030, 3036, 3040, 3052, 3060, 3078, 3080, 3084, 3102, 3108, 3114, 3120, 3126, 3132, 3138, 3144, 3150, 3168, 3172, 3174, 3186, 3192, 3198, 3204, 3222, 3234, 3246, 3249, 3258, 3270, 3276, 3282, 3294, 3306, 3318, 3330, 3336, 3360, 3366, 3378, 3388, 3390, 3408, 3430, 3432, 3450, 3462, 3474, 3498, 3500, 3510, 3516, 3522, 3534, 3552, 3558, 3570, 3582, 3588, 3594, 3606, 3608, 3618, 3624, 3636, 3640, 3642, 3654, 3660, 3672, 3702, 3714, 3726, 3732, 3738, 3744, 3762, 3768, 3770, 3774, 3780, 3786, 3798, 3810, 3816, 3822, 3828, 3840, 3846, 3858, 3864, 3870, 3876, 3882, 3894, 3900, 3906, 3918, 3930, 3936, 3942, 3952, 3954, 3960, 3966, 3976, 3978, 3984, 3990, 4002, 4004, 4008, 4014, 4020, 4026, 4032, 4060, 4068, 4080, 4088, 4092, 4098, 4100, 4107, 4108, 4110, 4116, 4134, 4140, 4144, 4146, 4152, 4158, 4172, 4182, 4200, 4206, 4208, 4218, 4224, 4228, 4242, 4272, 4278, 4284, 4290, 4302, 4314, 4320, 4326, 4344, 4350, 4362, 4374, 4380, 4386, 4396, 4416, 4428, 4434, 4446, 4452, 4458, 4470, 4482, 4494, 4506, 4508, 4512, 4518, 4520, 4530, 4542, 4554, 4560, 4580, 4584, 4590, 4602, 4614, 4626, 4636, 4638, 4640, 4644, 4650, 4662, 4664, 4668, 4674, 4680, 4686, 4692, 4698, 4704, 4710, 4714, 4716, 4720, 4722, 4728, 4734, 4736, 4746, 4752, 4758, 4770, 4776, 4778, 4782, 4792, 4794, 4798, 4812, 4818, 4854, 4860, 4866, 4878, 4890, 4896, 4902, 4912, 4914, 4926, 4938, 4950, 4954, 4956, 4962, 4974, 4980, 4984, 4986, 4998, 5004, 5010, 5012, 5016, 5022, 5028, 5034, 5040, 5044, 5046, 5056, 5058, 5064, 5068, 5076, 5080, 5082, 5092, 5104, 5106, 5118, 5124, 5130, 5136, 5160, 5164, 5178, 5180, 5190, 5208, 5214, 5220, 5226, 5232, 5236, 5238, 5244, 5256, 5262, 5268, 5274, 5280, 5286, 5290, 5298, 5310, 5314, 5340, 5348, 5352, 5364, 5368, 5376, 5382, 5388, 5404, 5406, 5418, 5430, 5436, 5442, 5454, 5460, 5466, 5468, 5478, 5480, 5490, 5496, 5502, 5510, 5514, 5520, 5526, 5532, 5538, 5548, 5550, 5552, 5556, 5560, 5562, 5568, 5574, 5586, 5588, 5592, 5598, 5610, 5646, 5658, 5670, 5674, 5680, 5682, 5694, 5704, 5706, 5712, 5718, 5720, 5724, 5730, 5740, 5742, 5748, 5754, 5760, 5766, 5778, 5784, 5790, 5792, 5802, 5808, 5814, 5816, 5818, 5820, 5826, 5838, 5840, 5844, 5850, 5852, 5856, 5862, 5870, 5872, 5874, 5886, 5896, 5904, 5914, 5916, 5922, 5934, 5940, 5970, 6006, 6018, 6020, 6024, 6030, 6042, 6056, 6058, 6060, 6068, 6072, 6074, 6080, 6098, 6102, 6108, 6116, 6132, 6140, 6150, 6168, 6170, 6172, 6180, 6186, 6188, 6192, 6196, 6198, 6200, 6204, 6210, 6222, 6228, 6234, 6246, 6250, 6252, 6258, 6264, 6270, 6276, 6284, 6288, 6294, 6304, 6330, 6338, 6344, 6348, 6364, 6366, 6372, 6378, 6388, 6390, 6396, 6408, 6414, 6424, 6426, 6432, 6438, 6440, 6444, 6450, 6462, 6474, 6482, 6486, 6492, 6496, 6500, 6510, 6520, 6522, 6524, 6528, 6546, 6558, 6564, 6570, 6576, 6580, 6582, 6590, 6594, 6604, 6618, 6624, 6630, 6632, 6642, 6654, 6656, 6660, 6666, 6676, 6678, 6680, 6696, 6700, 6702, 6714, 6720, 6726, 6732, 6738, 6750, 6752, 6756, 6762, 6768, 6774, 6780, 6784, 6786, 6792, 6796, 6798, 6810, 6822, 6828, 6832, 6834, 6846, 6860, 6870, 6888, 6894, 6896, 6902, 6904, 6906, 6908, 6916, 6918, 6930, 6936, 6938, 6940, 6942, 6948, 6986, 6996, 7014, 7020, 7028, 7040, 7044, 7050, 7060, 7062, 7064, 7074, 7080, 7084, 7086, 7088, 7092, 7098, 7122, 7128, 7134, 7140, 7144, 7146, 7148, 7152, 7158, 7170, 7172, 7182, 7184, 7188, 7192, 7194, 7206, 7208, 7212, 7216, 7218, 7224, 7225, 7228, 7240, 7242, 7254, 7256, 7260, 7268, 7272, 7274, 7281, 7296, 7302, 7308, 7314, 7326, 7332, 7338, 7344, 7350, 7356, 7360, 7362, 7372, 7374, 7384, 7386, 7388, 7392, 7398, 7404, 7410, 7416, 7422, 7434, 7436, 7446, 7450, 7464, 7470, 7490, 7494, 7504, 7506, 7516, 7518, 7530, 7532, 7534, 7554, 7556, 7560, 7566, 7570, 7572, 7578, 7584, 7588, 7600, 7602, 7620, 7632, 7638, 7644, 7656, 7662, 7664, 7668, 7670, 7674, 7676, 7680, 7684, 7686, 7690, 7692, 7696, 7704, 7712, 7722, 7728, 7732, 7736, 7740, 7754, 7764, 7776, 7780, 7782, 7788, 7794, 7806, 7808, 7818, 7820, 7824, 7828, 7830, 7842, 7844, 7848, 7852, 7854, 7864, 7866, 7868, 7872, 7878, 7880, 7890, 7902, 7908, 7920, 7922, 7924, 7936, 7944, 7956, 7960, 7962, 7974, 7980, 7982, 7984, 7986, 7992, 7998, 8002, 8004, 8010, 8016, 8020, 8022, 8028, 8032, 8046, 8052, 8054, 8056, 8058, 8064, 8068, 8082, 8084, 8088, 8094, 8096, 8112, 8114, 8118, 8120, 8124, 8130, 8142, 8144, 8152, 8154, 8160, 8166, 8170, 8172, 8178, 8184, 8196, 8216, 8226, 8240, 8252, 8256, 8274, 8280, 8286, 8288, 8298, 8300, 8304, 8310, 8316, 8324, 8326, 8334, 8340, 8344, 8350, 8352, 8360, 8364, 8370, 8372, 8376, 8382, 8394, 8396, 8406, 8408, 8410, 8412, 8416, 8424, 8430, 8440, 8442, 8448, 8454, 8456, 8460, 8466, 8484, 8490, 8512, 8514, 8526, 8528, 8538, 8540, 8544, 8550, 8562, 8568, 8574, 8576, 8580, 8584, 8586, 8588, 8592, 8596, 8598, 8600, 8604, 8610, 8622, 8624, 8628, 8634, 8640, 8646, 8650, 8652, 8658, 8676, 8680, 8682, 8684, 8686, 8688, 8692, 8694, 8706, 8708, 8718, 8720, 8730, 8732, 8736, 8742, 8744, 8748, 8754, 8760, 8764, 8766, 8772, 8778, 8780, 8788, 8790, 8796, 8808, 8816, 8820, 8824, 8832, 8844, 8848, 8850, 8856, 8862, 8864, 8874, 8876, 8880, 8886, 8890, 8898, 8904, 8910, 8922, 8930, 8934, 8942, 8944, 8946, 8952, 8964, 8976, 8996, 9018, 9028, 9034, 9036, 9042, 9044, 9052, 9054, 9064, 9066, 9070, 9078, 9088, 9096, 9102, 9110, 9114, 9116, 9126, 9132, 9136, 9138, 9140, 9144, 9150, 9152, 9160, 9162, 9174, 9176, 9180, 9186, 9198, 9200, 9210, 9212, 9222, 9228, 9230, 9232, 9234, 9244, 9252, 9256, 9258, 9268, 9270, 9274, 9282, 9290, 9292, 9294, 9296, 9302, 9306, 9312, 9318, 9320, 9324, 9330, 9342, 9344, 9348, 9352, 9360, 9372, 9384, 9396, 9400, 9402, 9404, 9412, 9414, 9420, 9440, 9450, 9462, 9466, 9468, 9474, 9486, 9490, 9496, 9498, 9510, 9526, 9534, 9542, 9548, 9554, 9558, 9564, 9570, 9576, 9578, 9582, 9592, 9594, 9606, 9612, 9614, 9618, 9630, 9636, 9642, 9644, 9654, 9656, 9660, 9666, 9670, 9672, 9678, 9680, 9690, 9692, 9702, 9712, 9720, 9728, 9762, 9768, 9774, 9780, 9782, 9784, 9796, 9812, 9818, 9822, 9834, 9836, 9844, 9846, 9852, 9856, 9870, 9880, 9882, 9884, 9888, 9894, 9900, 9902, 9906, 9916, 9918, 9924, 9928, 9930, 9942, 9950, 9954, 9958, 9960, 9962, 9966, 9980, 9996, 10002, 10008, 10010, 10012, 10014, 10018, 10022, 10026, 10036, 10038, 10040, 10044, 10048, 10050, 10052, 10062, 10068, 10076, 10080, 10084, 10086, 10088, 10092, 10094, 10096, 10098, 10104, 10110, 10120, 10122, 10124, 10128, 10134, 10136, 10146, 10152, 10154, 10158, 10160, 10170, 10190, 10202, 10208, 10212, 10218, 10220, 10224, 10230, 10244, 10248, 10252, 10254, 10258, 10260, 10264, 10266, 10276, 10278, 10284, 10286, 10296, 10302, 10320, 10324, 10328, 10332, 10348, 10362, 10364, 10374, 10382, 10384, 10386, 10392, 10398, 10410, 10422, 10424, 10428, 10434, 10444, 10446, 10452, 10458, 10466, 10470, 10480, 10486, 10488, 10490, 10492, 10500, 10506, 10514, 10516, 10520, 10536, 10542, 10544, 10548, 10554, 10556, 10564, 10566, 10572, 10578, 10584, 10590, 10592, 10600, 10602, 10614, 10620, 10626, 10636, 10640, 10644, 10650, 10656, 10662, 10674, 10676, 10680, 10684, 10686, 10692, 10698, 10700, 10704, 10706, 10710, 10722, 10728, 10732, 10734, 10736, 10746, 10748, 10752, 10758, 10764, 10770, 10776, 10782, 10792, 10794, 10800, 10804, 10806, 10808, 10812, 10818, 10820, 10822, 10824, 10830, 10836, 10840, 10848, 10854, 10860, 10864, 10868, 10880, 10888, 10896, 10912, 10914, 10920, 10926, 10928, 10940, 10944, 10954, 10956, 10968, 10974, 10976, 10986, 10988, 10990, 10992, 10998, 11000, 11004, 11010, 11014, 11016, 11020, 11022, 11025, 11026, 11034, 11040, 11044, 11046, 11052, 11058, 11060, 11070, 11072, 11076, 11080, 11082, 11086, 11090, 11094, 11096, 11100, 11104, 11110, 11114, 11116, 11118, 11130, 11132, 11136, 11142, 11148, 11154, 11160, 11166, 11172, 11180, 11184, 11196, 11200, 11202, 11204, 11206, 11208, 11212, 11214, 11220, 11222, 11224, 11244, 11256, 11262, 11274, 11280, 11282, 11286, 11292, 11304, 11308, 11310, 11316, 11320, 11322, 11326, 11334, 11336, 11340, 11346, 11352, 11356, 11358, 11360, 11364, 11380, 11382, 11388, 11402, 11406, 11408, 11418, 11424, 11430, 11432, 11434, 11442, 11448, 11450, 11454, 11460, 11466, 11468, 11474, 11478, 11480, 11484, 11490, 11512, 11514, 11520, 11524, 11526, 11532, 11536, 11538, 11540, 11550, 11556, 11562, 11564, 11568, 11570, 11574, 11586, 11592, 11616, 11620, 11622, 11626, 11628, 11634, 11646, 11652, 11658, 11670, 11680, 11682, 11688, 11694, 11698, 11700, 11704, 11706, 11708, 11718, 11728, 11730, 11734, 11736, 11738, 11740, 11754, 11756, 11764, 11766, 11772, 11778, 11784, 11792, 11802, 11808, 11810, 11816, 11818, 11820, 11824, 11832, 11838, 11840, 11842, 11848, 11850, 11856, 11860, 11862, 11868, 11872, 11874, 11876, 11880, 11886, 11896, 11898, 11910, 11922, 11928, 11934, 11936, 11944, 11946, 11952, 11956, 11958, 11970, 11972, 11976, 11982, 11994, 11996, 12006, 12012, 12018, 12028, 12030, 12038, 12042, 12052, 12054, 12060, 12066, 12068, 12076, 12078, 12088, 12090, 12102, 12106, 12114, 12124, 12144, 12150, 12156, 12160, 12162, 12174, 12180, 12184, 12186, 12192, 12204, 12208, 12210, 12216, 12222, 12224, 12226, 12228, 12234, 12236, 12246, 12248, 12250, 12256, 12258, 12264, 12270, 12274, 12282, 12292, 12300, 12306, 12316, 12320, 12321, 12332, 12336, 12342, 12348, 12354, 12356, 12366, 12368, 12372, 12376, 12378, 12380, 12388, 12390, 12393, 12394, 12400, 12402, 12404, 12414, 12420, 12426, 12438, 12440, 12460, 12462, 12472, 12474, 12476, 12480, 12486, 12490, 12492, 12494, 12498, 12504, 12510, 12512, 12518, 12520, 12522, 12524, 12528, 12530, 12532, 12534, 12546, 12558, 12560, 12570, 12572, 12576, 12580, 12584, 12594, 12596, 12600, 12602, 12606, 12612, 12616, 12618, 12624, 12628, 12630, 12640, 12642, 12648, 12650, 12652, 12654, 12660, 12664, 12670, 12672, 12680, 12688, 12694, 12696, 12702, 12708, 12712, 12714, 12718, 12722, 12736, 12738, 12742, 12744, 12750, 12774, 12780, 12782, 12786, 12788, 12792, 12798, 12804, 12808, 12810, 12814, 12816, 12822, 12826, 12832, 12834, 12842, 12846, 12848, 12858, 12862, 12864, 12870, 12882, 12884, 12888, 12894, 12908, 12912, 12918, 12920, 12924, 12930, 12936, 12950, 12956, 12960, 12964, 12966, 12978, 12980, 12988, 12990, 12994, 13000, 13002, 13020, 13026, 13030, 13032, 13036, 13038, 13042, 13044, 13048, 13056, 13062, 13074, 13086, 13088, 13096, 13098, 13104, 13110, 13112, 13120, 13124, 13128, 13134, 13140, 13148, 13150, 13152, 13154, 13156, 13158, 13160, 13164, 13168, 13182, 13194, 13202, 13206, 13225, 13228, 13232, 13236, 13240, 13242, 13246, 13248, 13254, 13260, 13266, 13272, 13278, 13284, 13286, 13288, 13296, 13306, 13308, 13310, 13312, 13314, 13320, 13326, 13338, 13342, 13346, 13350, 13352, 13356, 13360, 13362, 13368, 13372, 13374, 13380, 13386, 13388, 13398, 13400, 13410, 13414, 13416, 13420, 13424, 13430, 13436, 13440, 13452, 13458, 13462, 13464, 13470, 13478, 13480, 13482, 13484, 13488, 13500, 13504, 13506, 13510, 13512, 13518, 13526, 13530, 13534, 13542, 13554, 13562, 13566, 13572, 13578, 13586, 13588, 13590, 13596, 13598, 13600, 13602, 13614, 13624, 13626, 13632, 13638, 13640, 13648, 13650, 13658, 13660, 13662, 13670, 13674, 13680, 13684, 13686, 13688, 13689, 13698, 13702, 13704, 13708, 13710, 13714, 13718, 13728, 13740, 13744, 13746, 13752, 13758, 13770, 13776, 13782, 13784, 13788, 13792, 13794, 13798, 13812, 13816, 13818, 13820, 13824, 13830, 13839, 13854, 13858, 13864, 13866, 13878, 13880, 13884, 13888, 13890, 13896, 13902, 13904, 13908, 13910, 13914, 13916, 13920, 13926, 13938, 13940, 13944, 13950, 13962, 13964, 13966, 13974, 13980, 13986, 13988, 13992, 13998, 14004, 14008, 14012, 14016, 14022, 14070, 14072, 14088, 14096, 14100, 14114, 14122, 14124, 14130, 14134, 14136, 14142, 14154, 14168, 14172, 14178, 14180, 14182, 14184, 14190, 14200, 14202, 14212, 14220, 14224, 14226, 14230, 14236, 14238, 14240, 14250, 14256, 14262, 14270, 14274, 14286, 14290, 14296, 14298, 14304, 14310, 14320, 14328, 14334, 14340, 14342, 14346, 14358, 14360, 14364, 14370, 14376, 14394, 14406, 14412, 14420, 14424, 14426, 14430, 14432, 14436, 14442, 14454, 14460, 14466, 14474, 14476, 14478, 14484, 14499, 14500, 14504, 14506, 14508, 14510, 14520, 14526, 14532, 14538, 14542, 14544, 14550, 14552, 14556, 14562, 14568, 14574, 14580, 14586, 14588, 14608, 14610, 14616, 14620, 14624, 14632, 14644, 14646, 14648, 14652, 14658, 14660, 14664, 14668, 14670, 14678, 14680, 14684, 14686, 14692, 14704, 14712, 14716, 14718, 14720, 14730, 14738, 14742, 14754, 14760, 14764, 14766, 14780, 14790, 14804, 14808, 14812, 14820, 14838, 14840, 14844, 14850, 14852, 14856, 14862, 14864, 14866, 14874, 14880, 14888, 14892, 14896, 14898, 14900, 14904, 14910, 14932, 14934, 14938, 14946, 14948, 14956, 14960, 14968, 14974, 14976, 14982, 14986, 14988, 14994, 15002, 15006, 15008, 15016, 15020, 15024, 15028, 15032, 15039, 15040, 15042, 15054, 15058, 15062, 15066, 15068, 15070, 15072, 15078, 15080, 15084, 15088, 15090, 15092, 15102, 15108, 15110, 15120, 15128, 15140, 15142, 15150, 15152, 15156, 15180, 15186, 15190, 15192, 15196, 15198, 15200, 15210, 15216, 15228, 15232, 15234, 15244, 15246, 15252, 15258, 15264, 15266, 15268, 15270, 15272, 15294, 15300, 15302, 15306, 15312, 15318, 15320, 15324, 15330, 15342, 15344, 15346, 15354, 15362, 15366, 15368, 15374, 15378, 15384, 15392, 15400, 15402, 15408, 15410, 15420, 15426, 15428, 15432, 15438, 15444, 15450, 15460, 15468, 15474, 15486, 15490, 15492, 15504, 15510, 15512, 15526, 15534, 15540, 15548, 15560, 15564, 15582, 15588, 15590, 15592, 15594, 15596, 15598, 15600, 15618, 15620, 15625, 15628, 15630, 15632, 15634, 15640, 15642, 15644, 15646, 15648, 15652, 15654, 15666, 15672, 15674, 15676, 15678, 15680, 15682, 15688, 15696, 15700, 15702, 15714, 15732, 15740, 15744, 15748, 15750, 15754, 15760, 15764, 15786, 15788, 15790, 15798, 15800, 15804, 15808, 15810, 15816, 15820, 15822, 15828, 15834, 15838, 15840, 15844, 15846, 15852, 15856, 15858, 15864, 15866, 15870, 15872, 15886, 15892, 15906, 15912, 15918, 15924, 15928, 15936, 15940, 15944, 15946, 15948, 15952, 15964, 15972, 15984, 15992, 15996, 16000, 16002, 16010, 16014, 16016, 16020, 16028, 16032, 16034, 16048, 16062, 16064, 16074, 16080, 16104, 16106, 16108, 16112, 16116, 16118, 16122, 16128, 16132, 16134, 16136, 16140, 16146, 16148, 16156, 16158, 16160, 16162, 16168, 16170, 16186, 16194, 16204, 16206, 16212, 16218, 16222, 16224, 16226, 16230, 16234, 16236, 16248, 16252, 16258, 16264, 16266, 16272, 16274, 16280, 16284, 16292, 16296, 16300, 16320, 16332, 16334, 16336, 16338, 16344, 16348, 16350, 16362, 16374, 16378, 16386, 16390, 16392, 16394, 16396, 16398, 16404, 16410, 16422, 16428, 16434, 16452, 16472, 16474, 16484, 16488, 16494, 16500, 16502, 16506, 16508, 16512, 16516, 16518, 16520, 16524, 16528, 16530, 16534, 16536, 16540, 16548, 16564, 16590, 16594, 16596, 16602, 16604, 16610, 16614, 16632, 16638, 16640, 16650, 16660, 16662, 16674, 16676, 16680, 16684, 16686, 16694, 16696, 16698, 16704, 16710, 16716, 16724, 16734, 16738, 16742, 16744, 16746, 16752, 16756, 16758, 16762, 16768, 16772, 16776, 16782, 16794, 16800, 16806, 16818, 16824, 16828, 16830, 16832, 16836, 16840, 16842, 16844, 16854, 16860, 16864, 16866, 16868, 16872, 16876, 16882, 16884, 16890, 16892, 16896, 16910, 16914, 16916, 16920, 16926, 16930, 16938, 16940, 16946, 16948, 16950, 16962, 16972, 16974, 16976, 16978, 16980, 16984, 16986, 16990, 16994, 16996, 17016, 17022, 17026, 17028, 17030, 17032, 17034, 17040, 17048, 17052, 17056, 17060, 17068, 17072, 17074, 17080, 17082, 17092, 17096, 17098, 17106, 17108, 17116, 17118, 17124, 17128, 17130, 17136, 17142, 17144, 17146, 17148, 17154, 17160, 17162, 17166, 17168, 17172, 17178, 17184, 17190, 17194, 17196, 17204, 17208, 17212, 17214, 17216, 17226, 17232, 17236, 17238, 17240, 17250, 17252, 17260, 17262, 17272, 17274, 17276, 17278, 17286, 17288, 17290, 17292, 17294, 17308, 17318, 17320, 17328, 17332, 17346, 17352, 17354, 17358, 17362, 17368, 17376, 17378, 17382, 17388, 17392, 17394, 17418, 17420, 17430, 17432, 17452, 17454, 17456, 17460, 17466, 17468, 17472, 17476, 17478, 17482, 17502, 17510, 17514, 17518, 17522, 17524, 17528, 17538, 17550, 17560, 17570, 17572, 17576, 17578, 17580, 17592, 17598, 17600, 17604, 17610, 17612, 17616, 17620, 17622, 17628, 17630, 17640, 17642, 17650, 17658, 17660, 17664, 17666, 17670, 17674, 17676, 17688, 17690, 17700, 17704, 17718, 17720, 17722, 17728, 17730, 17736, 17742, 17748, 17750, 17754, 17766, 17772, 17774, 17780, 17782, 17784, 17802, 17804, 17808, 17812, 17818, 17820, 17832, 17844, 17848, 17850, 17858, 17874, 17880, 17882, 17886, 17888, 17896, 17898, 17904, 17906, 17910, 17912, 17922, 17934, 17936, 17940, 17946, 17952, 17960, 17964, 17968, 17970, 17980, 17982, 17986, 17988, 17990, 18000, 18002, 18010, 18012, 18024, 18032, 18034, 18036, 18040, 18042, 18048, 18072, 18082, 18084, 18098, 18108, 18110, 18114, 18116, 18124, 18126, 18132, 18134, 18138, 18150, 18158, 18160, 18162, 18170, 18172, 18174, 18176, 18180, 18186, 18188, 18198, 18200, 18210, 18212, 18216, 18220, 18222, 18224, 18234, 18236, 18246, 18248, 18256, 18258, 18260, 18266, 18268, 18274, 18276, 18282, 18284, 18294, 18306, 18312, 18314, 18316, 18318, 18320, 18324, 18330, 18340, 18342, 18346, 18352, 18354, 18356, 18366, 18372, 18378, 18384, 18388, 18390, 18396, 18400, 18412, 18418, 18420, 18426, 18428, 18436, 18438, 18440, 18444, 18450, 18452, 18454, 18456, 18468, 18474, 18480, 18482, 18486, 18504, 18508, 18516, 18520, 18522, 18534, 18538, 18540, 18542, 18544, 18546, 18550, 18552, 18558, 18564, 18568, 18570, 18574, 18586, 18588, 18590, 18592, 18594, 18600, 18608, 18612, 18616, 18618, 18620, 18624, 18630, 18634, 18642, 18644, 18648, 18650, 18672, 18682, 18684, 18690, 18698, 18704, 18706, 18708, 18710, 18714, 18718, 18724, 18726, 18730, 18732, 18738, 18750, 18752, 18756, 18760, 18762, 18769, 18778, 18780, 18784, 18792, 18794, 18796, 18808, 18814, 18816, 18822, 18826, 18832, 18834, 18844, 18846, 18848, 18858, 18868, 18870, 18874, 18876, 18880, 18886, 18894, 18900, 18912, 18918, 18920, 18924, 18926, 18930, 18942, 18946, 18950, 18966, 18972, 18978, 18984, 18990, 19002, 19014, 19026, 19028, 19032, 19038, 19050, 19062, 19064, 19068, 19074, 19076, 19078, 19084, 19096, 19100, 19102, 19110, 19112, 19120, 19122, 19124, 19128, 19130, 19134, 19140, 19160, 19162, 19164, 19170, 19176, 19180, 19182, 19184, 19206, 19218, 19230, 19234, 19236, 19240, 19242, 19244, 19248, 19254, 19256, 19260, 19264, 19266, 19272, 19276, 19278, 19280, 19288, 19290, 19300, 19304, 19306, 19316, 19324, 19332, 19344, 19346, 19354, 19356, 19362, 19374, 19378, 19384, 19386, 19390, 19392, 19394, 19400, 19412, 19414, 19416, 19422, 19424, 19430, 19434, 19436, 19446, 19452, 19458, 19460, 19464, 19468, 19470, 19480, 19482, 19484, 19488, 19492, 19494, 19496, 19504, 19506, 19512, 19516, 19518, 19530, 19540, 19542, 19554, 19562, 19566, 19576, 19578, 19590, 19592, 19599, 19604, 19608, 19612, 19644, 19648, 19660, 19666, 19668, 19670, 19674, 19676, 19698, 19704, 19712, 19716, 19720, 19726, 19734, 19742, 19746, 19750, 19752, 19754, 19758, 19760, 19770, 19780, 19788, 19792, 19794, 19800, 19806, 19816, 19818, 19820, 19830, 19836, 19842, 19854, 19860, 19866, 19872, 19878, 19880, 19890, 19894, 19896, 19902, 19904, 19932, 19936, 19948, 19952, 19960, 19972, 19974, 19986, 19988, 19990, 19992, 19998]'1
2
3
4
print("Time taken to compute classify_ali_seq_4(20000,m=30,i=1e9):")
%timeit classify_ali_seq_4(20000,m=30,i=1e9)
print("Time taken to compute classify_ali_seq_5(20000,m=30,i=1e9):")
%timeit classify_ali_seq_5(20000,m=30,i=1e9)
1
2
3
4
Time taken to compute classify_ali_seq_4(20000,m=30,i=1e9):
6.88 s ± 155 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Time taken to compute classify_ali_seq_5(20000,m=30,i=1e9):
1.11 s ± 26.2 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Observation
Considerable time difference (around 5 seconds)! Implementing the use of the memory did make the code a lot more efficient and free up the kernel, but it is important to note that this is at the cost of using memory.
Also, note that we do not consider 0 a perfect number. Even though it was tempting at first because it enters a loop of length 1, we decided that, since all natural numbers divide 0 and their sum is greater than 0, it could not be classified as a perfect number.
Some online research confirmed that its Aliquot Sequence is indeed undefined. To make graphs later on more clear, we initially took s(0)=0, so that Aliquot Sequences that terminate at 0 just produce more 0s. However, this produces more output. Also, cutting sequences short once they reach 0 also helped make our code more efficient later on, since it helps to find the term at which sequences reach 0 by simply looking at their length.
Therefore, we ignored 0 in all future questions, and if computed, s(0) returns “Undefined”.
Also, note that those numbers with sequences that exceed i must have terms that never repeat by definition, since otherwise they would enter a loop.
Now we check some of the values printed in each category to check whether the classification is correct:
1
print(aliquot_sequence(119))
1
[119, 25, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6]
1
print(aliquot_sequence(138))
1
[138, 150, 222, 234, 312, 528, 960, 2088, 3762, 5598, 6570, 10746, 13254, 13830, 19434, 20886, 21606, 25098, 26742, 26754, 40446, 63234, 77406, 110754, 171486, 253458, 295740, 647748, 1077612, 1467588]
1
print(aliquot_sequence(143))
1
[143, 25, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6]
1
print(aliquot_sequence(150))
1
[150, 222, 234, 312, 528, 960, 2088, 3762, 5598, 6570, 10746, 13254, 13830, 19434, 20886, 21606, 25098, 26742, 26754, 40446, 63234, 77406, 110754, 171486, 253458, 295740, 647748, 1077612, 1467588, 1956812]
1
print(aliquot_sequence(840))
1
[840, 2040, 4440, 9240, 25320, 51000, 117480, 271320, 765480, 1531320, 3721800, 7817640, 15635640, 32899560, 65799480, 139098120, 349027320, 699333000]
Looks good! All values behave as we would expect.
Observation
Note that a vast majority of numbers terminate at 0. This is probably because the sum of divisors tends to be smaller than the input number, and so we would expect most numbers’ Aliquot Sequences to tend to 0.
Also, there is a significant amount of numbers that reach term m with no clear pattern. Note that m here is just 30, so it is hard to tell how the proportion of each category would vary under larger m inputs. One could argue that, if given long enough, these would enter loops. However, from our random checks above, we see that some enter loops and some seem to be increasing.
Some of the limitations of this project are memory, processing speed of our computers and the kernel. If given better resources, we could investigate larger m inputs. However, our prediction is that the proportion would be very similar to the ones we have now if we ignore the last category. Even though many numbers that reached m=30 would probably enter loops or exceed i, there would still be a vast majority of numbers terminating at 0.
Now we explore some questions about Aliquot sequences:
Core Extension 1: Lengths of Loops
How long can the loop be if an aliquot sequence ends in a loop?
1
2
3
4
5
6
7
8
9
10
11
12
def loop_length(n, m=30, i=1e9):
"""
Given an n, returns the length of the loop of it Aliquot Sequence,
or None if there is no loop (for first m terms, if not exceeding i).
"""
aliq_seq = aliquot_sequence(n,m,i)
visited = {}
for j, term in enumerate(aliq_seq): # if a term is visited twice, must have a loop
if term in visited:
return j - visited[term] # counts how many terms between repeated terms for loop length
visited[term] = j
return None
1
loop_length(6)
1
1
1
loop_length(220)
1
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def max_loop_length(n, m, i=1e9, loop = False):
"""
This function finds the biggest loop length within the first m terms of the first n aliquot sequences.
When set to True, the Boolean variable 'loop' also gives the corresponding aliquot sequence.
"""
loop = []
length = []
for j in range(1, n):
if seq_detect_loop(j) == True: # finds loops
loop.append(j) # appends numbers whose Aliquot Sequences enter loops
length.append(loop_length(j)) # creates a list of their lengths to find the max
if loop == False: # only returns max length
return max(length)
else:
return f'{max(length)}, {aliquot_sequence(loop[length.index(max(length))], m, i)}' # max length and corresponding sequence
1
max_loop_length(20000, 100, 1e9, True)
1
'28, [7524, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444]'
1
2
3
4
print(aliquot_sequence(2856, 100, 1e9))
print(loop_length(2856, 100, 1e9))
print(aliquot_sequence(275444, 100, 1e9))
print(loop_length(275444, 100, 1e9))
1
2
3
4
[2856, 5784, 8736, 19488, 40992, 84000, 230496, 475356, 792484, 1013852, 1013908, 1058092, 1264340, 2049964, 2123576, 2778664, 3492536, 3077104, 2884816, 3391568, 3775384, 3303476, 3003244, 2288756, 1773484, 1558964, 1440718, 720362, 360184, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704]
28
[275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116, 31704, 47616, 83328, 177792, 295488, 629072, 589786, 294896, 358336, 418904, 366556, 274924, 275444, 243760, 376736, 381028, 285778, 152990, 122410, 97946, 48976, 45946, 22976, 22744, 19916, 17716, 14316, 19116]
28
Core Extension 2: Lengths of Terminating Sequences
If a sequence terminates at zero, how long can it be (relative to the starting $n$)?
Observation
As mentioned in Core Question 5, we initially took s(0)=0, so find_index1 had to be a bit more complex than just checking the length of the sequence to find the first 0.
We then realised this and created find_zero, which is more efficient. Again, we keep both to test their efficiency, but only the new versions are really needed.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def find_index1(aliq_seq, target, loop = False):
"""
Given an aliquot sequence and a target number, return the index at which the target number is first encountered,
or None if the target number is not in the sequence.
We include target as a variable so that we can recall it later if we want to investigate exceeding aliquot sequences.
"""
for i, item in enumerate(aliq_seq):
if item == target: # variable target in case we want to use this to investigate exceeding sequences
if loop == False:
return i+1 #i+1 since the ith index is the i+1th term in the sequence
else:
return i+1, aliq_seq # returns the index and corresponding sequence
return None
1
2
print(find_index1(aliquot_sequence(590,30), 0))
print(find_index1(aliquot_sequence(590,30), 0, loop = True))
1
2
12
(12, [590, 490, 536, 484, 447, 153, 81, 40, 50, 43, 1, 0])
1
2
3
4
5
6
7
8
9
def find_zero(n, m=30, i=1e9, loop = False):
"""
Given n, produces the first m terms of its Aliquot Sequence and returns the term index at which
it terminates at 0, or None if the sequence does not terminate at 0.
"""
u=aliquot_sequence(n,m,i)
if len(u) != m and u[-1] == 0: # either exceeding i or terminating, so we pick terminating
return len(u) # by checking the last term
return None
1
print(find_zero(1148, 73))
1
72
1
2
3
4
print("Time taken to compute find_index1(aliquot_sequence(590,30), 0):")
%timeit find_index1(aliquot_sequence(590,30), 0)
print("Time taken to compute find_zero(590):")
%timeit find_zero(590)
1
2
3
4
Time taken to compute find_index1(aliquot_sequence(590,30), 0):
3.47 µs ± 350 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Time taken to compute find_zero(590):
2.87 µs ± 136 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Observation
As we can see, our second function is slightly more efficient, so it was a good choice to change our code from producing a list of 0s until m terms are returned to cutting the sequence short once 0 is reached.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def terminator_zero(k, m=30, i=1e9, corresponding_seq = False, maximum = False):
"""
For the first k numbers, this function finds the Aliquot Sequences that terminate at 0
for the first m terms, and returns the term at which each sequence reaches 0.
If corresponding_seq is set to True, it also returns the corresponding sequence.
If maximum is set to True, it returns only the maximum index in the list,
i.e. the term at which the sequence reaches 0 for the sequence that takes the longest
to reach 0.
But if both are set to True, it just returns the longest
terminating sequence and its length until it reaches 0.
"""
terminator = classify_terminated(k,m,i) # picks terminating sequences
terminator_zero_list = [] # will contain the lengths of terminating sequences
for j in terminator:
terminator_zero_list.append(find_zero(j,m,i))
max_zero = max(terminator_zero_list) # finds the maximum length (to reach 0)
if corresponding_seq == False and maximum == False:
return terminator_zero_list # returns just a list of the lengths of terminating sequences
elif corresponding_seq == True and maximum == False:
return terminator, terminator_zero_list # also returns the corresponding numbers that give terminating sequences
elif corresponding_seq == False and maximum == True:
return max_zero # returns the maximum length
elif corresponding_seq == True and maximum == True:
return max_zero, aliquot_sequence(terminator[terminator_zero_list.index(max_zero)], m, i)
# returns the max and corresponding sequence
1
2
3
print(terminator_zero(200, 100, 1e9, True, True))
print(aliquot_sequence(180, 53))
print(len(terminator_zero(200, 100, 1e9, False, False)))
1
2
3
(53, [180, 366, 378, 582, 594, 846, 1026, 1374, 1386, 2358, 2790, 4698, 6192, 11540, 12736, 12664, 11096, 11104, 10820, 11944, 10466, 5236, 6860, 9940, 14252, 14308, 15218, 10894, 6746, 3376, 3196, 2852, 2524, 1900, 2440, 3140, 3496, 3704, 3256, 3584, 4600, 6560, 9316, 8072, 7078, 3542, 3370, 2714, 1606, 1058, 601, 1, 0])
[180, 366, 378, 582, 594, 846, 1026, 1374, 1386, 2358, 2790, 4698, 6192, 11540, 12736, 12664, 11096, 11104, 10820, 11944, 10466, 5236, 6860, 9940, 14252, 14308, 15218, 10894, 6746, 3376, 3196, 2852, 2524, 1900, 2440, 3140, 3496, 3704, 3256, 3584, 4600, 6560, 9316, 8072, 7078, 3542, 3370, 2714, 1606, 1058, 601, 1, 0]
191
Observation
So 191 out of the first 200 numbers terminate at zero! This is a very large proportion (makes sense from Core Question 5’s Observation).
Also, in the first 200 numbers, the longest legth of a terminating sequence is 53, for n=180. Therefore, terminating sequences’ lengths can be quite large compared to the starting number.
1
2
3
print(terminator_zero(2000, 100, 1e9, False, True))
print(terminator_zero(2000, 100, 1e9, True, True))
1
2
72
(72, [1148, 1204, 1260, 3108, 5404, 5460, 13356, 25956, 49756, 49812, 83244, 138964, 144326, 127978, 67322, 36250, 34040, 48040, 60140, 71572, 58208, 64264, 60836, 47692, 35776, 42456, 69144, 110376, 244824, 373356, 594884, 446170, 356954, 219706, 118874, 88720, 117740, 174916, 174972, 291844, 302666, 256438, 217322, 185014, 92510, 95626, 49274, 25894, 17198, 8602, 6950, 6070, 4874, 2440, 3140, 3496, 3704, 3256, 3584, 4600, 6560, 9316, 8072, 7078, 3542, 3370, 2714, 1606, 1058, 601, 1, 0])
1
2
print(aliquot_sequence(1148,72))
print(len(aliquot_sequence(1148,72)))
1
2
[1148, 1204, 1260, 3108, 5404, 5460, 13356, 25956, 49756, 49812, 83244, 138964, 144326, 127978, 67322, 36250, 34040, 48040, 60140, 71572, 58208, 64264, 60836, 47692, 35776, 42456, 69144, 110376, 244824, 373356, 594884, 446170, 356954, 219706, 118874, 88720, 117740, 174916, 174972, 291844, 302666, 256438, 217322, 185014, 92510, 95626, 49274, 25894, 17198, 8602, 6950, 6070, 4874, 2440, 3140, 3496, 3704, 3256, 3584, 4600, 6560, 9316, 8072, 7078, 3542, 3370, 2714, 1606, 1058, 601, 1, 0]
72
Observation
However, it seems that, as n gets bigger, the longest length for a terminating sequence grows more slowly. We can see this in 1148’s sequence, which has length 72 and is the longest terminating sequence in the first 2000 numbers. this is a big jump from 180’s sequence, but the length only went up from 53 to 72 (so n grew by about 6.38 times, while the length only grew by 1.36, a ratio of 0.21).
Extension 3: Plotting Aliquot Sequences
Now we find a nice way of plotting to visualise aliquot sequences which enter loops.
1
2
3
4
5
6
7
8
9
10
11
def plot_aliq_seq(n, m=30, i=1e9):
"""
Given an n, this function plots the first m terms of its Aliquot Sequence.
When called in a loop, this function plots all graphs in the same figure.
"""
x_vals = [j for j in range(0, len(aliquot_sequence(n,m, i)))] # first m numbers on x axis
y_vals = [aliquot_sequence(n,m,i)[j] for j in range(0, len(aliquot_sequence(n,m,i)))] # corresponding m terms on y axis
plt.plot(x_vals, y_vals) # plots them
plt.xlabel(f'Numbers 0 to {m}')
plt.ylabel(f'First {m} terms of {n} Aliquot Sequences')
#plt.show() #use this line if you want the plots to be generated separately
1
2
3
4
5
6
7
8
9
10
11
12
def plot_aliq_seq_show(n, m=30, i=1e9):
"""
Very similar to plot_aliq_seq.
Given an n, this function plots the first m terms of its Aliquot Sequence,
but when called in a loop this function plots each graph separately.
"""
x_vals = [j for j in range(0, len(aliquot_sequence(n,m,i)))]
y_vals = [aliquot_sequence(n,m,i)[j] for j in range(0, len(aliquot_sequence(n,m,i)))]
plt.plot(x_vals, y_vals)
plt.xlabel(f'Numbers 0 to {m}')
plt.ylabel(f'First {m} terms of {n} Aliquot Sequences')
plt.show() # this line plots the graphs separately
1
2
3
4
5
6
7
8
def plot_loops(k, m=30, i=1e9):
"""
For the first k numbers, this function plots the first m terms of looping Aliquot Sequences.
This function plots all graphs in the same figure.
"""
loop = classify_loops(k, m, i)
for j in range(0, len(loop)):
plot_aliq_seq(loop[j], m, i) # plots loops
1
2
3
4
5
6
7
8
9
def plot_loops_show(k, m=30, i=1e9):
"""
Similar to plot_loops.
For the first k numbers, this function plots the first m terms of looping Aliquot Sequences.
This function plots each graph separately.
"""
loop = classify_loops(k, m, i)
for j in range(0, len(loop)):
plot_aliq_seq_show(loop[j], m, i) # plots loops separately
1
2
plot_loops(100, 30, 1e9)
print(classify_loops(100, 30, 1e9))
1
[6, 25, 28, 95]
1
plot_loops(20000, 30)
1
plot_loops(20000, 30, 1e6)
1
plot_loops_show(563)
Note that graphs that are just a straight line show perfect numbers, graphs that enter a 2 loop show amicable numbers, and graphs that end in a straight line at zero represent sequences that terminate at zero.
1
plot_aliq_seq(2856, 200)
The longest loop, found in the question above (for 2856, of length 28).
1
plot_aliq_seq(12496, 30)
Observation
Note that this loop has length 5, so there are also odd lengthed loops.
1
2
3
4
5
6
7
8
9
10
def big_loop_lengths(k, m=30, big=2):
"""
For the first k numbers, this function returns a list of the numbers whose Aliquot Sequences
enter a loop (within the first m terms) of length exceeding input big.
"""
big_loops = []
for elt in classify_loops(k, m):
if loop_length(elt) > big:
big_loops.append(elt)
return big_loops # finds loops of longer lengths
1
2
3
4
5
6
7
8
def plot_big_loop_lengths(k, m=30, big=2):
"""
For the first k numbers, this function plots the first m terms of Aliquot Sequences
that enter a loop (within these first m terms) of length exceeding input big.
"""
big_loops = big_loop_lengths(k, m, big)
for elt in big_loops:
plot_aliq_seq(elt, m) # plots loops of longer length
1
plot_big_loop_lengths(100, 30, 0)
1
plot_big_loop_lengths(500, 30, 1)
1
plot_big_loop_lengths(30000)
1
2
3
4
5
6
7
8
def plot_terminated(k, m=30, i=1e9):
"""
For the first k numbers, this function plots the first m terms of Aliquot Sequences
that terminate at 0 (within these first m terms).
"""
terminated = classify_terminated(k, m, i)
for elt in terminated:
plot_aliq_seq(elt, m, i) # plots terminating sequences
1
2
plot_terminated(100)
print(classify_terminated(100))
1
[1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 96, 97, 98, 99, 100]
1
2
3
4
5
6
7
8
def plot_exceeded(k, m=30, i=1e9):
"""
For the first k numbers, this function plots the first m terms of Aliquot Sequences
that exceed input i within these first m terms.
"""
exceeded = classify_exceeded(k, m, i)
for elt in exceeded:
plot_aliq_seq(elt, m, i) # plots exceeding sequences
1
plot_exceeded(2000, 30, 1e9)
1
2
3
4
5
6
7
8
def plot_reached_term(k, m=30, i=1e9):
"""
For the first k numbers, this function plots the first m terms of Aliquot Sequences
that reached term m without exceeding input i, entering a loop or terminating at 0.
"""
reached_term = classify_reached_term(k, m, i)
for j in range(1, len(reached_term)):
plot_aliq_seq(reached_term[j], m, i) # plots sequences that reach term m with no clear pattern
1
2
print(classify_reached_term(1000,30,1e9))
plot_reached_term(1000, 30, 1e9)
1
[138, 150, 168, 180, 210, 222, 234, 264, 276, 306, 312, 318, 330, 354, 360, 366, 378, 396, 456, 480, 498, 510, 528, 534, 546, 552, 564, 570, 582, 594, 600, 612, 642, 654, 660, 696, 702, 720, 726, 750, 780, 786, 798, 822, 828, 834, 846, 858, 864, 870, 888, 930, 936, 960, 966, 978, 990, 996]
Extension 4: Perfect, Amicable, Adbundant and Deficient Numbers
As stated above, perfect numbers are numbers such that $s(n)=n$, i.e. 6, which has proper divisors 1, 2, 3, and $1+2+3=6$, so $s(6)=6$.
Related to perfect numbers are ‘abundant’ numbers with $s(n) > n$ and ‘deficient’ numbers, where $s(n) < n$. A looping aliquot sequence should contain some of each.
We will compare the number of each up to a fixed value n.
Since this question was of great interest to our group, we divided it into 6 parts to carry out further investigations.
Part A: Perfect Numbers
We create functions to determine whether a number is perfect, and to find perfect numbers up to a given k.
1
2
3
4
5
6
7
8
def is_perfect(n):
"""
Given a number n, this function returns True if it a perfect number
and False if not.
"""
if s(n)==n: # checks the definition of perfect numbers
return True
return None
1
2
3
4
5
6
7
8
9
def find_perfect_numbers(k):
"""
For an input k, this function returns a list of the perfect numbers in the first k numbers.
"""
perfect = []
for i in range(0, k):
if is_perfect(i) == True:
perfect.append(i)
return perfect
1
is_perfect(6)
1
True
1
find_perfect_numbers(100)
1
[6, 28]
1
s(28)
1
28
1
find_perfect_numbers(20000)
1
[6, 28, 496, 8128]
Observation
As we can see, perfect numbers are incredibly scarce.
From online research, we discovered that every perfect number can be written in the form $2^{p-1} (2^p - 1)$, where p and $2^p - 1$ are both prime numbers. Therefore, the conditions for perfect numbers are quite specific and rare, giving rise to a very low proportion of them amongst the integers.
Part B: Amicable Numbers
Here, we find 2 ways, of varying efficiencies, to find amicable numbers.
1
2
3
4
5
6
7
8
def is_amicable(a,b):
"""
Given two numbers a and b, this function returns True if they are an
amicable pair of numbers and False if not.
"""
if s(a)==b and s(b)==a and a != b: # checks the definition of amicable numbers, excluding perfect numbers
return True
return None
1
print(is_amicable(6,6))
1
None
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def find_amicable_numbers(k):
"""
For an input k, this function returns a list of pairs of amicable numbers in the first k numbers.
However, it is a very inefficient function because it has a for loop within a for loop,
and it checks whether i and j are amicable for all numbers, essentially sorting through k^2 numbers.
"""
amicable = []
for i in range(1, k):
for j in range(1, k):
if is_amicable(i, j) == True: # finds amicable pairs and perfect numbers
amicable.append([i,j])
for elt in amicable:
if is_perfect(elt[0]) == True: # removes perfect numbers
amicable.remove(elt)
for elt1 in amicable:
for elt2 in amicable:
if sum(elt1) == sum(elt2): # for pairs with the same sum, they must be the same pair in reverse order
amicable.remove(elt1) # so this removes the repeats in descending order
return amicable
1
is_amicable(220, 284)
1
True
1
find_amicable_numbers(1000)
1
[[284, 220]]
1
2
3
#find_amicable_numbers(20000)
#Keyboard Interrupt error because has to be stopped/ breaks down the kernel.
#Too slow! We will need to create a more efficient (and amicable ;) ) function.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def efficient_and_amicable(k): #that's me!
"""
For an input k, this function finds the looping Aliquot Sequences within
the first k numbers. Since amicable numbers must enter loops of length 2, it then
picks such loops. Also, amicable numbers must be the first 2 terms of such length 2 loops,
so the function checks whether the first and third terms in the sequence are the same.
It returns a list of such pairs of numbers and deletes duplicates, as well as the length
of this list (the number of amicable pairs within the first k Aliquot Sequences).
"""
too_amicable = [] # will contain all numbers that enter a loop of length 2
amicable = [] # will contain only amicable pairs
loops = classify_loops(k)
for elt in loops:
if loop_length(elt) == 2: # finds all loops of length 2
too_amicable.append(elt)
for elt in too_amicable:
if aliquot_sequence(elt)[0] == aliquot_sequence(elt)[2]: # checks whether the loops start at the first term,
amicable.append(sorted([elt, s(elt)])) # i.e. whether the number is amicable
for elt in amicable:
while amicable.count(elt) > 1: # removes repeats
amicable.remove(elt)
length = len(amicable)
return f"{amicable} \n \n{length}" # returns amicable pairs and the number of pairs
1
print(efficient_and_amicable(300))
1
2
3
[[220, 284]]
1
1
print(efficient_and_amicable(20000))
1
2
3
[[220, 284], [1184, 1210], [2620, 2924], [5020, 5564], [6232, 6368], [10744, 10856], [12285, 14595], [17296, 18416]]
8
1
print(efficient_and_amicable(1000000))
1
2
3
[[220, 284], [1184, 1210], [2620, 2924], [5020, 5564], [6232, 6368], [10744, 10856], [12285, 14595], [17296, 18416], [66928, 66992], [67095, 71145], [67095, 71145], [63020, 76084], [69615, 87633], [79750, 88730], [122368, 123152], [100485, 124155], [122265, 139815], [141664, 153176], [141664, 153176], [142310, 168730], [171856, 176336], [176272, 180848], [196724, 202444], [185368, 203432], [280540, 365084], [280540, 365084], [308620, 389924], [356408, 399592], [319550, 430402], [437456, 455344], [469028, 486178], [503056, 514736], [522405, 525915], [643336, 652664], [667964, 783556], [600392, 669688], [609928, 686072], [624184, 691256], [635624, 712216], [667964, 783556], [726104, 796696], [802725, 863835], [879712, 901424], [947835, 1125765], [898216, 980984], [998104, 1043096]]
46
1
2
3
4
print("Time taken to compute find_amicable_numbers(1000):")
%timeit find_amicable_numbers(1000)
print("Time taken to compute efficient_and_amicable(1000):")
%timeit efficient_and_amicable(1000)
1
2
3
4
Time taken to compute find_amicable_numbers(1000):
188 ms ± 4.23 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Time taken to compute efficient_and_amicable(1000):
3.12 ms ± 164 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Observation
The second function is significantly more efficient! Using our understanding of mathematics in this question and finding amicable numbers through loops of length 2 starting at the first term instead of checking all sums of divisors and comparing where they give pairs made the code nearly 70 times more efficient.
Also, note that they are again a quite scarce type of number. We have 5 perfect numbers vs 8 amicable pairs in the first 20000 numbers, so from this we believe there are more amicable than perfect numbers, but not by too much.
From online research, we found that this may be because the set of amicable numbers is a proper subset of the set of sociable numbers, which are also rare due to the specific properties that their divisors that must have (must be cyclical, i.e. their Aliquot Sequences enter loops where the sum of divisors are terms of the sequence, and there are already significantly less loops than integers, so it is not surprising that these are rare, and hence amicable numbers rarer).
Part C: Abundant and Deficient Numbers: Ratio Amongst the Integers
We will investigate which numbers up to k are abundant or deficient, and their comparison in a ratio.
1
2
3
4
5
6
7
8
9
10
def is_abundant(n):
"""
Given a number n, this function returns True if it an abundant number
and False if not.
"""
if s(n)=="Undefined": # ignores n=0
return False
elif s(n)>n: # checks the definition of abundant numbers
return True
return False
1
2
3
4
5
6
7
8
9
def find_abundant_numbers(k):
"""
For an input k, this function returns a list of the abundant numbers in the first k numbers.
"""
abundant = []
for j in range(1, k+1):
if is_abundant(j) == True:
abundant.append(j)
return abundant
1
2
3
4
5
6
7
8
9
10
def is_deficient(n):
"""
Given a number n, this function returns True if it a deficient number
and False if not.
"""
if s(n)=="Undefined": # ignores n=0
return False
elif s(n)<n: # checks the definition of abundant numbers
return True
return False
1
2
3
4
5
6
7
8
9
def find_deficient_numbers(k):
"""
For an input k, this function returns a list of the deficient numbers in the first k numbers.
"""
deficient = []
for j in range(1, k+1):
if is_deficient(j) == True:
deficient.append(j)
return deficient
1
2
3
4
5
6
7
8
def compare_ab_and_def(k):
"""
For an input k, this function compares the amount of abundant and deficient numbers
within the first k numbers.
"""
ab_num = len(find_abundant_numbers(k))
def_num = len(find_deficient_numbers(k))
return f'Up to k={k}, there are {ab_num} abundant numbers vs {def_num} deficient numbers.'
1
print(is_deficient(6))
1
False
1
compare_ab_and_def(1000)
1
'Up to k=1000, there are 246 abundant numbers vs 750 deficient numbers.'
1
compare_ab_and_def(20000)
1
'Up to k=20000, there are 4953 abundant numbers vs 15042 deficient numbers.'
Observation
From testing our function above, we can see there are usually around 3 times as many deficient numbers than abundant ones. This makes sense because of how numbers are constructed- divisors will be smaller than the number itself, and adding numbers gives a smaller (or equal (for 2x2)) result than multiplying them, so on average the sum of divisors is likely to be smaller than the actual number.
Also, as seen above, most numbers terminate at zero, so it is sensible to think that it is a lot more likely that the sum of divisors tends to zero, i.e. there are more deficient numbers.
Part D: Abundant and Deficient Numbers: Existence
We investigate whether all Aliquot Sequences have some abundant and deficient numbers (at least 1 of each), and if not which type of number doesn’t.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def exists_abundant(n, m=30, i=1e9):
"""
Given a number n, this function checks the first mth terms in its aliquot sequence
to ascertain whether there exists a term that is an abundant number.
It returns True if it does, and False if not.
"""
ab_loop = []
u = aliquot_sequence(n, m, i)
for j in u:
if is_abundant(j) == True:
ab_loop.append(j) # creates list of abundant terms
if len(ab_loop) == 0: # if the length is 0, list is empty, so no abundant terms
return False
else:
return True
1
exists_abundant(6)
1
False
1
exists_abundant(220, 30)
1
True
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def exists_deficient(n, m=30, i=1e9):
"""
Given a number n, this function checks the first mth terms in its aliquot sequence
to ascertain whether there exists a term that is a deficient number.
It returns True if it does, and False if not.
"""
def_loop = []
u = aliquot_sequence(n, m, i)
for j in u:
if is_deficient(j) == True:
def_loop.append(j) # creates list of deficient terms
if len(def_loop) == 0: # if the length is 0, list is empty, so no deficient terms
return False
else:
return True
1
exists_deficient(6)
1
False
1
exists_deficient(220, 30)
1
True
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def are_there_ab_and_def(k, m=30, i=1e9, perfect=True):
"""
Up to the first k numbers, this function finds the looping aliquot sequences
and then checks whether all of these contain both abundant and deficient numbers
within the first m terms.
If perfect is set to False, the code does not account for perfect numbers or perfect loops
(since they are less interesting, as perfect numbers have neither abundant nor deficient terms
and perfect loops are likely to be entirely deficient until the perfect number).
"""
count_both=0 # a count for the number of sequences including both abundant and deficient terms
not_exist_both = 0 # and for those including neither
not_both = True
for j in range(1, k+1):
if perfect == False:
if loop_length(j) != 1: # this excludes perfect numbers and perfect loops
if exists_abundant(j, m, i) and exists_deficient(j, m, i) == True:
count_both += 1
else:
not_exist_both +=1
not_both = False
elif perfect == True:
if exists_abundant(j, m, i) and exists_deficient(j, m, i) == True:
count_both += 1 # if True, we don't need to check how many have neither
else:
not_exist_both +=1 # but if False, we count them and return a comparison of how many had both
not_both = False # and how many had neither
if not_both == False:
return False, f"There are {count_both} numbers with some abundant and deficient terms, and {not_exist_both} numbers without both."
else:
return True
1
2
print(are_there_ab_and_def(2000))
print(are_there_ab_and_def(2000, 30, 1e9, False))
1
2
(False, 'There are 966 numbers with some abundant and deficient terms, and 1034 numbers without both.')
(False, 'There are 960 numbers with some abundant and deficient terms, and 1010 numbers without both.')
1
2
print(are_there_ab_and_def(200000))
print(are_there_ab_and_def(200000, 30, 1e9, False))
1
2
(False, 'There are 90729 numbers with some abundant and deficient terms, and 109271 numbers without both.')
(False, 'There are 90381 numbers with some abundant and deficient terms, and 108173 numbers without both.')
Observation
Recall we took perfect numbers to be a subset of looping numbers.
Since it is clear that perfect numbers do not have either abundant or deficient terms, we exclude them from our general investigation. We also exclude numbers with sequences ending in perfect numbers (perfect loops), since those may be only deficient until they reach the perfect number.
When set to False, our function returns similar outputs. From the difference, we can see that around 1 in every 200 numbers is either pefect or enters a perfect loop. Since we know perfect numbers are scarce, this means perfect loops are also scarce but less so.
As we can see, the test for 200000 outputs False. This means there are not always both some abundant and deficient numbers in Aliquot Sequences, and it is (around 1.2 times) more common.
Part E: Abundant and Deficient Numbers: Looping Aliquot Sequences
Now we investigate the ratio of abundant to deficient numbers within loops of Aliquot Sequences.
1
print(classify_loops(1000))
1
[6, 25, 28, 95, 119, 143, 220, 284, 417, 445, 496, 562, 565, 608, 650, 652, 675, 685, 783, 790, 909, 913]
1
2
3
4
5
6
7
8
9
10
11
12
def abundant_loop(n, m=30, i=1e9):
"""
Given n, this function produces the first m terms of a looping Aliquot Sequence
and returns only the abundant numbers.
"""
ab_loop = []
u = aliquot_sequence(n, m, i)
if seq_detect_loop(n) == True: # checks if there is a loop
for j in u:
if is_abundant(j) == True: # checks if there is an abundant term
ab_loop.append(j)
return ab_loop
1
2
print(abundant_loop(220))
print(aliquot_sequence(220))
1
2
[220, 220, 220, 220, 220, 220, 220, 220, 220, 220, 220, 220, 220, 220, 220]
[220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284]
1
2
3
4
5
6
7
8
9
10
11
12
def deficient_loop(n, m=30, i=1e9):
"""
Given n, this function produces the first m terms of a looping Aliquot Sequence
and returns only the deficient numbers.
"""
def_loop = []
u = aliquot_sequence(n, m)
if seq_detect_loop(n) == True: # checks if there is a loop
for j in u:
if is_deficient(j) == True: # checks if there is a deficient term
def_loop.append(j)
return def_loop
1
2
print(deficient_loop(220))
print(aliquot_sequence(220))
1
2
[284, 284, 284, 284, 284, 284, 284, 284, 284, 284, 284, 284, 284, 284, 284]
[220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284, 220, 284]
1
2
3
4
5
6
7
8
9
def compare_ab_and_def_loop(n, m=30, i=1e9):
"""
Given n, this function produces the first m terms of a looping Aliquot Sequence
and returns a comparison of the amount of abundant numbers vs deficient numbers.
"""
ab_len = len(abundant_loop(n,m,i))
def_len = len(deficient_loop(n,m,i))
# compares the lengths of abundant and deficient lists
return f'There are {ab_len} abundant terms vs {def_len} deficient terms in the first {m} terms of the Aliquot Sequence for {n}.'
1
compare_ab_and_def_loop(220)
1
'There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 220.'
1
compare_ab_and_def_loop(2856)
1
'There are 0 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 2856.'
1
compare_ab_and_def_loop(12496, 1500)
1
'There are 600 abundant terms vs 900 deficient terms in the first 1500 terms of the Aliquot Sequence for 12496.'
1
2
3
4
5
6
7
8
9
def compare_many_ab_and_def_loops(k, m=30, i=1e9, big=1):
"""
For an input k, this function finds the first m terms of the looping Aliquot Sequences
within the first k numbers with loop lengths exceeding input big.
It returns a comparison of the amount of abundant numbers vs deficient numbers in each of these sequences.
"""
big_loops = big_loop_lengths(k, m, big)
for j in big_loops:
print(compare_ab_and_def_loop(j,m,i))
1
compare_many_ab_and_def_loops(1000,30,0)
1
2
3
There are 1 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 220.
There are 0 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 284.
There are 0 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 562.
1
compare_many_ab_and_def_loops(10000,30)
Click to expand
There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 220. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 284. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 562. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 1064. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 1184. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 1188. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 1210. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 1308. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 1336. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 1380. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 1420. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 1490. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 1604. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 1690. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 1692. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 1772. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 1816. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 1898. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 2008. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 2122. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 2152. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 2172. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 2362. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 2542. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 2620. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 2630. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 2652. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 2676. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 2678. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 2924. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 2930. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 2950. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 2974. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3124. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3162. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3202. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3278. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3286. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3332. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 3350. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3596. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3712. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3750. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3850. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 3938. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 3944. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 4118. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 4156. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 4180. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 4372. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 4404. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 4448. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 4522. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 4790. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 4840. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 4930. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 5020. There are 12 abundant terms vs 18 deficient terms in the first 30 terms of the Aliquot Sequence for 5024. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 5078. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 5150. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 5234. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 5380. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 5564. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 5622. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 5630. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 5634. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 5854. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 5890. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 5900. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 5942. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 5960. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 6028. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 6036. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 6232. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 6242. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 6280. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 6368. There are 12 abundant terms vs 18 deficient terms in the first 30 terms of the Aliquot Sequence for 6420. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 6532. There are 12 abundant terms vs 18 deficient terms in the first 30 terms of the Aliquot Sequence for 6612. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 6658. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 6694. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 6808. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 6872. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 6876. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7006. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7106. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7120. There are 12 abundant terms vs 18 deficient terms in the first 30 terms of the Aliquot Sequence for 7130. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 7180. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7186. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 7294. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7380. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7418. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 7514. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7520. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 7524. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 7540. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7694. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7796. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 7860. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7930. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 7940. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 8076. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 8104. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 8306. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 8320. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 8354. There are 12 abundant terms vs 18 deficient terms in the first 30 terms of the Aliquot Sequence for 8480. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 8776. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 8784. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 8924. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 9038. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 9068. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 9204. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 9322. There are 12 abundant terms vs 18 deficient terms in the first 30 terms of the Aliquot Sequence for 9332. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 9370. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 9464. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 9484. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 9550. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 9572. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 9574. There are 13 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 9620.1
2
3
4
5
6
7
8
9
10
def many_loop_lengths(k, m=30, i=1e9):
"""
This function outputs a list of the lengths of all looping Aliquot Sequences
within the first k numbers (and m terms without exceeding i).
"""
loop_lengths=[]
loops = classify_loops(k,m,i)
for j in loops:
loop_lengths.append(loop_length(j,m,i))
return loop_lengths
1
print(many_loop_lengths(20000))
1
[1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 2, 2, 1, 1, 2, 2, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 1, 2, 2, 2, 2, 2, 1, 2, 1, 1, 1, 2, 1, 1, 2, 1, 1, 2, 2, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 1, 2, 2, 1, 2, 2, 1, 2, 1, 2, 1, 1, 2, 1, 2, 2, 2, 1, 1, 2, 2, 1, 2, 1, 2, 2, 1, 2, 2, 2, 2, 1, 1, 1, 1, 1, 2, 2, 1, 2, 2, 2, 2, 2, 1, 2, 1, 2, 2, 1, 1, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 2, 2, 28, 1, 2, 1, 1, 2, 2, 1, 28, 1, 1, 2, 2, 2, 2, 1, 1, 2, 2, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 2, 2, 28, 1, 2, 2, 2, 5, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 2, 1, 2, 1, 1, 1, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 2, 1, 2, 2, 1, 5, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 5, 2, 1, 2, 1, 2, 2, 1, 1, 2, 2, 2, 1, 1, 1, 2, 2, 2, 1, 2, 1, 1, 1, 2, 2, 2, 1, 2, 1, 1, 1, 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 5, 1, 1, 5, 28, 2, 2, 2, 2, 1, 1, 1, 5, 2, 1, 2, 2, 1, 2, 2, 2, 2, 1, 2, 1, 2, 2, 1, 2, 5, 5, 2, 2, 2, 2, 2, 2, 2, 1, 2, 1, 1, 1, 2, 2, 2, 2, 2, 1, 2, 1, 2, 2, 2, 1, 2, 5, 1, 1, 1, 2, 2, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 1, 2, 2, 2, 1, 28, 2, 1, 1, 2, 1, 28, 1, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 2, 1, 2, 28, 2, 2, 2, 2, 2, 5, 2, 2, 2, 28, 2, 1, 2, 1, 2, 2, 1, 2, 1, 2, 1, 2, 2, 28, 2, 1, 2, 2, 1]
1
2
print(compare_ab_and_def_loop(12496))
print(aliquot_sequence(12496))
1
2
There are 12 abundant terms vs 18 deficient terms in the first 30 terms of the Aliquot Sequence for 12496.
[12496, 14288, 15472, 14536, 14264, 12496, 14288, 15472, 14536, 14264, 12496, 14288, 15472, 14536, 14264, 12496, 14288, 15472, 14536, 14264, 12496, 14288, 15472, 14536, 14264, 12496, 14288, 15472, 14536, 14264]
Observation
Again, it is of great value to our investigation to take perfect numbers as loops.
When testing for the comparison of abundant to deficient numbers in looping Aliquot Sequences, we drew 2 distinctions.
Firstly, we can see that most looping Aliquot Sequences of even length have a very similar amount of abundant and deficient numbers. This makes sense, since once they enter the loop, they must cycle between a finite number of numbers, out of which half are likely to be abundant and half deficient (because, clearly, not all can be abundant, since the sequence would exceed i, or deficient, since the sequence would terminate at zero). Hence their ratio is nearly a perfect 50/50. However, for odd length cycles, the opposite happens. In the case of perfect numbers, there will be 0 of each, but for numbers that end in perfect numbers they are likely to have a larger number of deficient numbers, accounting for the first terms, that are likely to decrease until the perfect number is reached and the loop of length 1 entered. In the case of 12496, we can see the ratio is 40/60. This is because it has a cycle of length 5, out of which 2 are abundant and 3 deficient, giving the exact ratio. Nonetheless, we can note that, from checking the function many_loop_lengths, most loops are either length 1, which are not as interesting, or even length. Hence, it is still reasonable to claim that looping Aliquot Sequences have a similar number of abundant and deficient terms.
Secondly, when only considering the first m=30, the ratio may not be as close to 50/50, again to account for the first terms until the loop is entered. But for larger m this becomes negligible.
Note that we created a functions, compare_ab_and_def_loop, specific to loops when we could have be created a general function for any Aliquot Sequence (which we do in the next cell). Though these could be combined into just the second function since they do similar things, we were more interested in investigating loops, so we kept both for efficiency when only interested in calling loops.
Part F: Abundant and Deficient Numbers: General Aliquot Sequences
Similar to before, we investigate the ratio of abundant to deficient numbers within Aliquot Sequences, but now they do not have to necessarily enter loops.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def compare_ab_and_def_seq(n, m=30, i=1e9):
"""
Given n, this function produces the first m terms of Aliquot Sequence
and returns a comparison of the amount of abundant numbers vs deficient numbers.
"""
u= aliquot_sequence(n,m,i)
ab_list=[]
def_list=[]
for elt in u:
if is_abundant(elt) == True:
ab_list.append(elt)
elif is_deficient(elt) == True:
def_list.append(elt)
# creates lists of abundant and deficient numbers to compare their lengths
ab_len=len(ab_list)
def_len=len(def_list)
print(f'There are {ab_len} abundant terms vs {def_len} deficient terms in the first {m} terms of the Aliquot Sequence for {n}.')
return ab_len, def_len
1
2
print(compare_ab_and_def_seq(52))
print(aliquot_sequence(52))
1
2
3
There are 0 abundant terms vs 8 deficient terms in the first 30 terms of the Aliquot Sequence for 52.
(0, 8)
[52, 46, 26, 16, 15, 9, 4, 3, 1, 0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def test_compare(n):
"""
This function produces a comparison of the amount
of abundant numbers vs deficient numbers in n random Aliquot Sequences
(n between 0 and 1000000, randomly generated).
"""
more_def=0
more_ab=0
for j in range(n):
j=random.randint(0,1000000) # for random numbers, counts the number of abundant and deficient terms in their sequences
compare_ab_and_def_seq(j)
if compare_ab_and_def_seq(j)[0]<compare_ab_and_def_seq(j)[1]:
more_def += 1
elif compare_ab_and_def_seq(j)[0]>compare_ab_and_def_seq(j)[1]:
more_ab += 1
return f'There are {more_def} with more deficient numbers, and {more_ab} with more abundant numbers.' # returns comparison
1
test_compare(100)
Click to expand
There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 733793. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 733793. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 733793. There are 3 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 807070. There are 3 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 807070. There are 3 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 807070. There are 29 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 512840. There are 29 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 512840. There are 29 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 512840. There are 29 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 512840. There are 29 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 512840. There are 16 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 364714. There are 16 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 364714. There are 16 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 364714. There are 16 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 364714. There are 16 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 364714. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 227196. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 227196. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 227196. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 227196. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 227196. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 703255. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 703255. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 703255. There are 2 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 527152. There are 2 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 527152. There are 2 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 527152. There are 5 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 584608. There are 5 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 584608. There are 5 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 584608. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 722871. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 722871. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 722871. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 835688. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 835688. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 835688. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 91387. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 91387. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 91387. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 76766. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 76766. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 76766. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 130679. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 130679. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 130679. There are 6 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 493030. There are 6 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 493030. There are 6 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 493030. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 105294. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 105294. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 105294. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 105294. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 105294. There are 9 abundant terms vs 21 deficient terms in the first 30 terms of the Aliquot Sequence for 227994. There are 9 abundant terms vs 21 deficient terms in the first 30 terms of the Aliquot Sequence for 227994. There are 9 abundant terms vs 21 deficient terms in the first 30 terms of the Aliquot Sequence for 227994. There are 18 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 970204. There are 18 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 970204. There are 18 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 970204. There are 18 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 970204. There are 18 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 970204. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 533675. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 533675. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 533675. There are 0 abundant terms vs 8 deficient terms in the first 30 terms of the Aliquot Sequence for 658809. There are 0 abundant terms vs 8 deficient terms in the first 30 terms of the Aliquot Sequence for 658809. There are 0 abundant terms vs 8 deficient terms in the first 30 terms of the Aliquot Sequence for 658809. There are 7 abundant terms vs 12 deficient terms in the first 30 terms of the Aliquot Sequence for 618479. There are 7 abundant terms vs 12 deficient terms in the first 30 terms of the Aliquot Sequence for 618479. There are 7 abundant terms vs 12 deficient terms in the first 30 terms of the Aliquot Sequence for 618479. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 951291. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 951291. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 951291. There are 2 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 8156. There are 2 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 8156. There are 2 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 8156. There are 22 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 253386. There are 22 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 253386. There are 22 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 253386. There are 22 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 253386. There are 22 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 253386. There are 0 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 553603. There are 0 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 553603. There are 0 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 553603. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 464237. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 464237. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 464237. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 414838. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 414838. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 414838. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 961062. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 961062. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 961062. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 961062. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 961062. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 276733. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 276733. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 276733. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 426017. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 426017. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 426017. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 418136. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 418136. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 418136. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 418136. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 418136. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 633836. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 633836. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 633836. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 633836. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 633836. There are 25 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 465194. There are 25 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 465194. There are 25 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 465194. There are 25 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 465194. There are 25 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 465194. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 21961. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 21961. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 21961. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 35286. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 35286. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 35286. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 35286. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 35286. There are 2 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 682138. There are 2 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 682138. There are 2 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 682138. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 902854. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 902854. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 902854. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 189006. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 189006. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 189006. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 189006. There are 19 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 189006. There are 0 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 386103. There are 0 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 386103. There are 0 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 386103. There are 24 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 719178. There are 24 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 719178. There are 24 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 719178. There are 24 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 719178. There are 24 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 719178. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 389117. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 389117. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 389117. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 508255. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 508255. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 508255. There are 2 abundant terms vs 8 deficient terms in the first 30 terms of the Aliquot Sequence for 669562. There are 2 abundant terms vs 8 deficient terms in the first 30 terms of the Aliquot Sequence for 669562. There are 2 abundant terms vs 8 deficient terms in the first 30 terms of the Aliquot Sequence for 669562. There are 10 abundant terms vs 20 deficient terms in the first 30 terms of the Aliquot Sequence for 386424. There are 10 abundant terms vs 20 deficient terms in the first 30 terms of the Aliquot Sequence for 386424. There are 10 abundant terms vs 20 deficient terms in the first 30 terms of the Aliquot Sequence for 386424. There are 30 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 859962. There are 30 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 859962. There are 30 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 859962. There are 30 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 859962. There are 30 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 859962. There are 18 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 49968. There are 18 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 49968. There are 18 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 49968. There are 18 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 49968. There are 18 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 49968. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 564233. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 564233. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 564233. There are 15 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 201758. There are 15 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 201758. There are 15 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 201758. There are 15 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 201758. There are 15 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 201758. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 497351. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 497351. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 497351. There are 3 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 21794. There are 3 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 21794. There are 3 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 21794. There are 6 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 962026. There are 6 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 962026. There are 6 abundant terms vs 24 deficient terms in the first 30 terms of the Aliquot Sequence for 962026. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 431207. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 431207. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 431207. There are 9 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 942816. There are 9 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 942816. There are 9 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 942816. There are 9 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 942816. There are 9 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 942816. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 724780. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 724780. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 724780. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 724780. There are 16 abundant terms vs 14 deficient terms in the first 30 terms of the Aliquot Sequence for 724780. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 702974. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 702974. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 702974. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 302303. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 302303. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 302303. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 185204. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 185204. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 185204. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 185204. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 185204. There are 27 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 200154. There are 27 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 200154. There are 27 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 200154. There are 27 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 200154. There are 27 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 200154. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 515617. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 515617. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 515617. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 564807. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 564807. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 564807. There are 1 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 216055. There are 1 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 216055. There are 1 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 216055. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 793231. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 793231. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 793231. There are 0 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 160773. There are 0 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 160773. There are 0 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 160773. There are 2 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 836872. There are 2 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 836872. There are 2 abundant terms vs 17 deficient terms in the first 30 terms of the Aliquot Sequence for 836872. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 203103. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 203103. There are 0 abundant terms vs 2 deficient terms in the first 30 terms of the Aliquot Sequence for 203103. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 677297. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 677297. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 677297. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 971327. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 971327. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 971327. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 631982. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 631982. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 631982. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 631982. There are 21 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 631982. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 136437. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 136437. There are 0 abundant terms vs 4 deficient terms in the first 30 terms of the Aliquot Sequence for 136437. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 716875. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 716875. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 716875. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 928505. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 928505. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 928505. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 620709. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 620709. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 620709. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 728688. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 728688. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 728688. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 803534. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 803534. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 803534. There are 15 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 960618. There are 15 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 960618. There are 15 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 960618. There are 15 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 960618. There are 15 abundant terms vs 0 deficient terms in the first 30 terms of the Aliquot Sequence for 960618. There are 2 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 10609. There are 2 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 10609. There are 2 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 10609. There are 18 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 914040. There are 18 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 914040. There are 18 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 914040. There are 18 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 914040. There are 18 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 914040. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 93276. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 93276. There are 11 abundant terms vs 19 deficient terms in the first 30 terms of the Aliquot Sequence for 93276. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 39626. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 39626. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 39626. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 39626. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 39626. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 226784. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 226784. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 226784. There are 6 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 548110. There are 6 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 548110. There are 6 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 548110. There are 11 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 85752. There are 11 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 85752. There are 11 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 85752. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 763045. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 763045. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 763045. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 138679. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 138679. There are 0 abundant terms vs 1 deficient terms in the first 30 terms of the Aliquot Sequence for 138679. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 610379. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 610379. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 610379. There are 3 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 37609. There are 3 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 37609. There are 3 abundant terms vs 7 deficient terms in the first 30 terms of the Aliquot Sequence for 37609. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 568099. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 568099. There are 0 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 568099. There are 19 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 631960. There are 19 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 631960. There are 19 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 631960. There are 19 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 631960. There are 19 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 631960. There are 0 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 590723. There are 0 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 590723. There are 0 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 590723. There are 5 abundant terms vs 12 deficient terms in the first 30 terms of the Aliquot Sequence for 30624. There are 5 abundant terms vs 12 deficient terms in the first 30 terms of the Aliquot Sequence for 30624. There are 5 abundant terms vs 12 deficient terms in the first 30 terms of the Aliquot Sequence for 30624. There are 3 abundant terms vs 25 deficient terms in the first 30 terms of the Aliquot Sequence for 972112. There are 3 abundant terms vs 25 deficient terms in the first 30 terms of the Aliquot Sequence for 972112. There are 3 abundant terms vs 25 deficient terms in the first 30 terms of the Aliquot Sequence for 972112. There are 0 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 31305. There are 0 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 31305. There are 0 abundant terms vs 11 deficient terms in the first 30 terms of the Aliquot Sequence for 31305. There are 24 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 685760. There are 24 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 685760. There are 24 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 685760. There are 24 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 685760. There are 24 abundant terms vs 5 deficient terms in the first 30 terms of the Aliquot Sequence for 685760. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 745954. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 745954. There are 7 abundant terms vs 23 deficient terms in the first 30 terms of the Aliquot Sequence for 745954. There are 1 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 564477. There are 1 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 564477. There are 1 abundant terms vs 9 deficient terms in the first 30 terms of the Aliquot Sequence for 564477. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 780913. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 780913. There are 0 abundant terms vs 3 deficient terms in the first 30 terms of the Aliquot Sequence for 780913. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 145650. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 145650. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 145650. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 145650. There are 20 abundant terms vs 10 deficient terms in the first 30 terms of the Aliquot Sequence for 145650. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 968366. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 968366. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 968366. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 968366. There are 15 abundant terms vs 15 deficient terms in the first 30 terms of the Aliquot Sequence for 968366. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 658306. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 658306. There are 8 abundant terms vs 22 deficient terms in the first 30 terms of the Aliquot Sequence for 658306. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 863652. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 863652. There are 14 abundant terms vs 16 deficient terms in the first 30 terms of the Aliquot Sequence for 863652. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 627187. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 627187. There are 0 abundant terms vs 6 deficient terms in the first 30 terms of the Aliquot Sequence for 627187.1
'There are 72 with more deficient numbers, and 25 with more abundant numbers.'
Observation
Now we see that the ratio of abundant to deficient numbers in Aliquot Sequences is no longer so evenly split- outside of loops, deficient numbers become more common again with approximately a 70/30 ratio.
Extension 5: The Preimage
For a fixed n, we will investigate how large the preimage $s^{−1}({n})$ can be.
This should tell us something about when aliquot sequences starting at different values merge together.
We could think of 2 ways of doing this: Either use the memory to count the numbers that appear most in s(n) for the first n numbers, or produce the preimages by checking s(j) up until a function of j that ensures we didn’t miss any elements in the preimage.
However, using the second method was too time consuming, and finding such a function was very difficult. We include our attempt at the end for the curious reader, but the first method was enough to carry out the question’s investigation.
It could also be interesting to study partitions to create a function that gives multiplies the largest possible multiplication of sums to return the largest possible element in a number’s preimage.
Observation
First off, we can already see that 1 is a very uninteresting number. Its preimage will be infinite, since $\forall$ prime numbers p, $s(p)=1$ by definition, and there are infinitely many prime numbers (by Euclid’s Theorem). Hence, in our function below we introduce a Boolean variable to ignore 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
def preimage(n, k):
"""
Given an n, computes its preimage with elements less than or equal to k.
Note that for the purposes of this investigation,
choosing a big k is enough, but it would be ideal to find a
function of n that tells us what the maximum preimage element can be.
"""
preim = []
for j in range(1, k+1):
if s(j) == n:
preim.append(j)
return preim
1
2
def preimage_size(n,k):
return len(preimage(n,k))
1
print(preimage(284, 20000))
1
[220, 562]
1
2
print(preimage(1,1000))
print(len(preimage(1, 1000)))
1
2
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
168
1
print(preimage(2, 100))
1
[]
Observation
Makes sense that $s^{-1}(2)=\emptyset$ since we have $\forall n \in \mathbb{N}, 1 \in s^{-1}(n)$, so $2-1=1 \implies$ only other divisor would also have to be 1, but $1(1)=1 \neq 2$.
1
2
3
4
5
6
7
8
9
def many_preimages(k, big = 2):
small_size = []
bigger = []
for j in range(1, k+1):
if preimage_size(j,k)>=big: # checks preimage size is big
bigger.append(j)
else:
small_size.append(j)
return f"There are {len(small_size)} with preimages of size 0 or 1, and {len(bigger)} with size {big} or more."
1
print(many_preimages(100))
1
There are 83 with preimages of size 0 or 1, and 17 with size 2 or more.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def max_preimage_size(k, which = False, ignore_1 = False):
"""
Checks, by using the memory, which number appears
most commonly in s(k) for the first k numbers.
If which is set to True, it also tells us which numbers are the most common,
i.e. the numbers the maximum count correspond to, and their preimage.
If ignore_1 is set to True, it does this ignoring 1, since it always have the biggest preimage.
Note: If ignore_1 is set to False, this function basically computes the
number of prime numbers in the first k numbers, and can also return a list of them.
"""
preim_count={0:0} # using a dictionary instead of a list to keep track of the corresponding numbers to the max_count
for j in range(1, k+1):
preim_count[j]=len(preimage(j,k)) # appends the sizes of the preimages
max_count = max(preim_count.values()) # finds the maximum preimage size
max_keys = [j for j, count in preim_count.items() if count == max_count]
# finds the corresponding numbers with this size of preimage
if ignore_1 == True:
for c in max_keys:
del preim_count[c] # removes 1 and its preimage value from the dictionary
max_count = max(preim_count.values()) # finds new maximum
if which == True:
reverse = {count: preim for preim, count in preim_count.items()} # reverses dictionary to be able to call the key
# corresponding to the maximum value
max_preim = [j for j, count in preim_count.items() if count == max_count] # finds the number with this max preimage size
return max_count, max_preim # returns both the maximum preimage size and the corresponding number
return max_count # otherwise, returns only the maximum preimage size
1
2
3
4
5
6
print(max_preimage_size(100))
print(max_preimage_size(100, True, False))
print(max_preimage_size(100, False, True))
print(max_preimage_size(100, True, True))
print(preimage(21, 100))
print(preimage(40, 100))
1
2
3
4
5
6
25
(25, [1])
3
(3, [21, 40])
[18, 51, 91]
[44, 74, 81]
1
max_preimage_size(1000, True, True)
1
(6, [49, 55, 61, 65])
1
2
print(aliquot_sequence(49))
preimage(49, 1000)
1
2
3
4
5
6
7
[49, 8, 7, 1, 0]
[75, 215, 287, 407, 527, 551]
1
max_preimage_size(20000, True, True)
1
(20, [211, 241])
1
2
3
4
print(preimage(211, 20000))
print(preimage(241, 20000))
print(aliquot_sequence(211))
print(aliquot_sequence(241))
1
2
3
4
[338, 2189, 2561, 3281, 3629, 5249, 5549, 6401, 7181, 7661, 8321, 8909, 9089, 9869, 10001, 10349, 10541, 10961, 11009, 11021]
[399, 1127, 1631, 2519, 2951, 3791, 6119, 8159, 8471, 9071, 10679, 10919, 11591, 12191, 13031, 13439, 14039, 14111, 14279, 14351]
[211, 1, 0]
[241, 1, 0]
1
2
3
4
y0 = [75, 215, 287, 407, 527, 551]
print("Aliquot Sequences merging at 49.")
for y in y0:
plot_aliq_seq(y, m=30, i=1e9)
1
Aliquot Sequences merging at 49.
1
2
3
4
5
6
y0 = [49, 55, 61, 65]
print("Aliquot Sequences merging at 49, 55, 61, 65 (preimages of size 6).")
for y in y0:
preim = preimage(y, 1000)
for j in preim:
plot_aliq_seq(j, m=30, i=1e9)
1
Aliquot Sequences merging at 49, 55, 61, 65 (preimages of size 6).
1
2
3
4
y1 = [338, 2189, 2561, 3281, 3629, 5249, 5549, 6401, 7181, 7661, 8321, 8909, 9089, 9869, 10001, 10349, 10541, 10961, 11009, 11021]
print("Aliquot Sequences merging at 211.")
for y in y1:
plot_aliq_seq(y, m=30, i=1e9)
1
Aliquot Sequences merging at 211.
1
2
3
4
y2 = [399, 1127, 1631, 2519, 2951, 3791, 6119, 8159, 8471, 9071, 10679, 10919, 11591, 12191, 13031, 13439, 14039, 14111, 14279, 14351]
print("Aliquot Sequences merging at 241.")
for y in y2:
plot_aliq_seq(y, m=30, i=1e9)
1
Aliquot Sequences merging at 241.
1
2
print(aliquot_sequence(399))
print(aliquot_sequence(1127))
1
2
[399, 241, 1, 0]
[1127, 241, 1, 0]
Observation
We can see that the size of the preimage of n, $|s^{-1}(n)|$, grows very slowly as n increases (from a maximum size of 6 $\approx log(1000)$ in the first 1000 numbers to 20 in the first 20000, i.e. $|s^{-1}(n)|$ increased by 3.33 times when n increased by 20, a ratio of 0.167.
From online research, we found that it has been proved that the maximum preimage size up to n is roughly proportional to the logarithm of n, with order of growth of log(n)/log(log(n)) (Erdős and Pomerance, 1986). It is interesting to see how intricately related the natural log is in number theory, as we can recall that the Prime Number Theory also states the number of prime numbers up to a given N is approximately $N/log(N)$.
Thus, the preimage size of any positive integer n will be very small compared to n’s size.
Of course, this is excluding 1, which has an infinitely large preimage.
Therefore, we can conlude that it is very uncommon for Aliquot Sequences to merge (except at 1, and then 0, which explains why so many numbers have Aliquot Sequences terminating at 0). This is because for 2 Aliquot Sequences to merge, they must have an equal term, i.e. a term with a preimage size of 2 or bigger. Such numbers are much less common than those with preimages of size 0 or 1 (as we saw 17 vs 83 in the first 100 numbers).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def preimage_s(n):
"""
For a given n, this function finds the preimage of s(n).
"""
preimage = []
if n == 1:
for i in range(1, 100): # for 1, since preimage is infinite, checks elements less than 100
if s(i) == n:
preimage.append(i)
return preimage
else:
for i in range(1, n**2-n): # the reason behind this range is explained in the observation below
if s(i) == n: # checks numbers that give n when function s is applied, i.e. the preimage definition
preimage.append(i)
return preimage
In the code above, we check the numbers up until $n^2$ to see whether the sum of their divisors gives our input n.
This is because the sum of a number’s divisors is always less than or equal to $2\sqrt n$, so checking $n^2 - n$ (sincen is not a proper divisor) for the inverse seems appropriate to find numbers that fall in the preimage of n. (Except for 1. Then we check the first 100 to check our function with the output above.)
Also, suppose you have a list of the partitions of n. We want to find all the m’s such that s(m)=n, and we know one of the partitions will be exactly the divisors of m. The sum of pairs of divisors is at most n+1 $\forall n \in \mathbb{N}$, and there can be at most n-1 proper divisors. If we multiply each element in the list of partitions by each number up to n-1, we are guaranteed to hit m, and thus we can find the preimage. Since the biggest element in the partitions of n is just the list $[n]$, we can approximate this by giving an upper bound of $n(n-1) = n^2 - n$. This is why we check i this range above.
1
2
print(preimage_s(1))
print(len(preimage_s(1)))
1
2
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
25
1
preimage_s(220)
1
[284]
1
preimage_s(284)
1
[220, 562, 80089]
1
s(80089)
1
284
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def preimage_size2(k, preim = False):
"""
This function finds the largest size of the preimage of s(k) for the first k numbers.
"""
size = [] # list of sizes to find the maximum
for i in range(1, k+1):
size_i = len(preimage_s(i))
size.append(size_i)
max_size = max(size)
max_index = []
for i in size:
if i == max_size:
max_index.append(size.index(i)+1) # finds the index i, appends i+1 since is the i+1th term
if preim == False:
return max_size # returns only the max size
if preim == True:
slist = [s(elt) for elt in max_index]
preimage_slist = [preimage_s(elt) for elt in max_index]
return max_size, max_index, slist, preimage_slist # also returns the max indeces, the function s applied to them,
# and the preimages
1
2
print(preimage_size2(100))
print(preimage_size2(100, True))
1
2
25
(25, [1], ['Undefined'], [[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]])
1
preimage_s(245)
1
[723, 1195, 2563, 3859, 9259, 10123, 12283, 14659, 14803]
1
print(preimage_s(623))
1
[1857, 3085, 13777, 17197, 30157, 33217, 52621, 57517, 64321, 77677, 79297, 82321, 90637, 91537, 94417, 94957]
1
print(preimage_s(1079))
1
[18037, 30421, 48457, 60121, 98677, 103897, 124057, 128917, 138421, 152137, 169417, 173557, 200521, 207577, 210997, 217621, 223957, 241237, 258121, 271477, 276121, 278857, 284437, 286921, 288217, 289621, 290197]
1
# preimage_size(10000, True) code runs too slowly
1
2
3
4
print("Time taken to compute max_preimage_size(100):")
%timeit max_preimage_size(100)
print("Time taken to compute preimage_size2(100):")
%timeit preimage_size2(100)
1
2
3
4
Time taken to compute max_preimage_size(100):
1.07 ms ± 11.5 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Time taken to compute preimage_size2(100):
46.4 ms ± 729 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
Observation
As we can see, our second method and function is about 40 times slower. However, it is more exhaustive and accurate: It is slow because it checks too many numbers, but note that it did include 80089 in the preimage of 284, whereas our first function didn’t.
1
2
3
4
5
6
def primes(k):
prime_list = []
for j in range(1, k+1):
if isprime_basic(j) == True:
prime_list.append(j)
return prime_list
1
print(primes(100))
1
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
1
2
3
4
print("Time taken to compute primes(100):")
%timeit primes(100)
print("Time taken to compute preimage(1,100):")
%timeit preimage(1,100)
1
2
3
4
Time taken to compute primes(100):
27.2 µs ± 1.12 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Time taken to compute preimage(1,100):
12 µs ± 306 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Observation
Our function is 2 times more effiecient than isprime_basic! Even though computing primes in this way is not at all efficient, and our function was only faster due to the advantage of using the memory (when most prime functions use it too), it is still a cool result of our investigation.
Conclusion:
Through the use of the memory, dynamic programming and mathematics, we managed to create functions to answer each question that run pretty efficiently. Our main observations were the following:
· A vast majority of Aliquot Sequences terminate at 0, due to how numbers are constructed.
· Loops do not tend to have very long lengths (the longest one we found had length 28, for 2856, 7524, 275444, etc).
· Terminating sequences can be quite long relative to the starting n (the longest one we found had length 72, for 1148).
· Perfect numbers are very scarce, with only 4 in the first 20,000, and amicable numbers are also scarce but less so, with only 46 pairs in the first 1,000,000 numbers.
· While the ratio is nearly 50/50 for looping sequences of even length, other loops and general sequences, as well as the integers themselves, show a preference for deficient numbers. Again, this is because of how numbers are constructed.
· The size of the preimage grows very slowly as n increases (with order log(n)/log(log(n))). This means that not many Aliquot Sequences starting at different values merge together.
· Aliquot Sequences are fun! Thank you for marking :)
More Developed Conclusions
For the interested reader:
Why are there more deficient numbers?
One reason there are more deficient numbers than any other type in Aliquot Sequences is because of how many prime numbers exist, particularly in the early integers. This is of course influential as the sum of proper divisors of a prime number is just 1. As mentioned, this is mainly a contributing factor when looking at Aliquot sequences that start at smaller numbers (for example between 1 and 500). This is because the proportion of prime numbers inevitably gets smaller as you increase the range in which you are looking for them. To show this, by tallying up the prime numbers between 1 and 500, we get that there are 95 of them. This is 19% of 500, therefore almost one-fifth of the numbers up to 500 are deficient without even considering other cases of numbers.
The more general reason why there are more deficient numbers in Aliquot sequences, which encases the argument above, is that it is less common for a number to have large enough factors to be abundant or even perfect. An abundant number would need to be divisible by a high enough proportion of numbers between 2 and 10 to get large enough proper divisors. For example, 360 is divisible by 2, 3, 4, 5, 6, 8, and 10 so is comfortably an abundant number. However, this is quite rare, if we consider numbers that are divisible by 2 and 3, so very likely to be abundant, we see that this is one in every 6 numbers and so a significant minority.
Why are there a similar number of Abundant and Deficient numbers in a looping Aliquot sequence?
The reason there is a similar number of Abundant and Deficient numbers in a looping Aliquot sequence is simply because the sequence must return to the number at the start of the loop. This is much clearer through an example. Suppose you have a loop of length n that starts at a number $x_1$. There are 3 cases:
1) If x is a perfect number, then the loop is of length n = 1 and the number of abundant and deficient numbers are both equal to 0.
2) If x is a deficient number, then the next term in the sequence $x_2 < x_1$ and so we will need the sequence to increase again to return to $x_1$. Thus somewhere along the next n-1 terms we will require a term in the sequence will have the property that $x_i+1 > x_i$, for some $i = 2, 3, … , n$. This implies that this $x_i$ is an abundant number. This does not guarantee that the number of abundant and deficient numbers will be equal, but they will certainly be similar.
3) If x is an abundant number, then the next term in the sequence $x_2 > x_1$ and using the same reasoning as in 2), we require that some $x_i$, for $i = 2, 3, … , n$ is a deficient number. This again creates a similar number of abundant and deficient numbers in our looping Aliquot sequence.